1. Найти максимальное и минимальное значение функции f(x,y)=x^2+2x+y^2+2y+6 на множестве x^2+y^2<=8
Смотреть решение
2. На плоскости прямоугольных декартовых координат (x, y) расположен эллипс с центром в начале координат и полуосями \( 1/\sqrt{3},1/3 \) Известно, что большая ось эллипса образует угол \( \alpha=arccos(1/\sqrt{3}) \)с осью абсцисс (угол отсчитывается от оси абсцисс против часовой стрелки). Найти уравнение эллипса в координатах (x, y).
Смотреть решение
3. Написать процедуру или функцию, которая печатает в стандартный вывод два различных наименьших ключа двоичного дерева поиска (считать, что в параметре – дереве
поиска содержится не менее двух вершин и нет вершин с равными ключами). Сравнение
ключей не выполнять ни явно, ни неявно. Тип двоичного дерева поиска (tree) описан
следующим образом:

Смотреть решение
4. Дано тело реляционного отношения с первичным ключом {№Чека, №Позиции}:
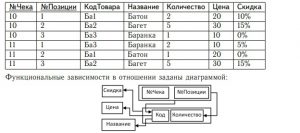
1) Укажите самую старшую из нормальных форм, в которых находится данное отношение. В ответе следует привести обоснование. 2) Используя теорему Хита, выполните для данного отношения декомпозицию без потерь на независимые проекции так, чтобы все полученные отношения находились в третьей нормальной форме, и чтобы количество полученных отношений было минимальным. В ответе выпишите тела отношений, полученных после декомпозиции.
Смотреть решение
5. Найти решение y(x) задачи Коши yy”+1=(y’)^2;y(2)=1/2,y'(2)=√3/2
Смотреть решение
6. Выделить из полной в множестве P2 всех булевых функций системы
\( A={f(x1,x2),g(x1,x2,x3),h(x1,x2,x3)} \)
все базисы (т. е. неизбыточные полные системы) в P2, если векторы значений функций f, g, h имеют вид соответственно \( α_{f} \) = (0111), \( α_{g} \) = (00010111), \( α_{h} \) = (10010110). Ответ обосновать.
Смотреть решение
7. Случайная величина ξ имеет плотность \( f_{ξ}(x)=Ce^{-2|x|} \)Вычислить константу C и найти плотность случайной величины \( η=e^{3ξ} \)
8. Найти набор параметров θk ∈ [0, 1], k = 1, 2, . . . , N, при которых квадратурная формула
\( I_{h}=\sum\limits_{k=1}^nf(θ_{k}x_{k} + (1 − θ_{k})x_{k}−1)(x_{k} − x_{k}−1)) \), a = x0 < x1 < x2 < . . . < xN = b для вычисления интеграла \( I=\int_{a}^{b}f(x)dx \) точна для произвольной функции из семейства \( f(x)=\alpha x^3+\beta \), \( \alpha,\beta=const \)
Смотреть решение
9. Решить задачу utt=uxx/16 , -∞<x<∞, t>0; u(x,0)=4cos3x; ut(x,0)=3sin3x
Смотреть решение
