13. Дано уравнение log2(4cosx)^2-8log2(2cosx)+3=0
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку {-7П/2;-2П}
Посмотреть решение
14. В основании пирамиды лежит равнобедренный треугольник АВС, в
котором АВ=4, BAC =120 . Известно, что боковая грань SBC перпендикулярна
основанию АВС, SB=SC, а высота пирамиды, проведенная из точки S, равна 112 . На
ребрах SB и SC отмечены соответственно точки К и Р так, что ВК:SK=CP:SP=1:3.
А) Докажите, что сечением пирамиды плоскостью АРК является прямоугольный
треугольник.
Б) Найдите объем меньшей части пирамиды, на которые её делит плоскость АРК.
Решение: первая часть, вторая часть.
15. Решить уравнение
![]()
Посмотреть решение
16. В параллелограмме АВСD диагональ ВD равна стороне AD.
А) Докажите, что прямая СD касается окружности ω, описанной около треугольника
АВD.
Б) Пусть прямая СВ вторично пересекает ω в точке К. Найдите КD:AC при условии, что
угол ВDA равен 120.
Посмотреть решение
17. В начале января 2018 года планируется взять кредит в банке на 4 года на S млн.
рублей, где S – целое число. Условия его возврата таковы:
‐ каждый июль долг возрастает на 10% по сравнению с началом текущего года;
‐ с августа по декабрь каждого года необходимо выплатить часть долга;
‐ в январе каждого года долг должен составлять часть кредита в соответствии со
следующей таблицей: ![]()
Найдите наименьшее значение S, при котором сумма выплат банку за все 4 года
составит не менее 10 млн. рублей.
Посмотреть решение
18.
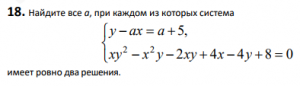
Решение: первая часть, вторая часть, третья часть.
19. Дано двузначное натуральное число.
а) Оказалось, что частное этого числа и суммы его цифр, равно 7. Найдите все такие
числа.
б) Какие натуральные значения может принимать частное данного числа и суммы его
цифр?
в) Какое наименьшее значение может принимать частное данного числа и суммы его
цифр?
Посмотреть решение
Реклама
