1. В доме, в котором живёт Катя, 12 этажей и несколько подъездов. На каждом этаже в каждом подъезде находится по 6 квартир. Катя живёт в квартире 261. На каком этаже живёт Катя?
Смотреть решение
3. Найдите площадь параллелограмма, вершины которого имеют координаты (4; 7), (7; 6), (4; 10), (7; 9).
Смотреть решение
4. Гигрометр измеряет влажность в помещении картинной галереи. Вероятность того, что влажность окажется выше 40 %, равна 0,78. Вероятность того, что влажность окажется ниже 55 %, равна 0,68. Найдите вероятность того, что влажность находится в пределах от 40 % до 55 %.
Смотреть решение
5. Найдите корень уравнения \( \sqrt{5x}=2*\frac{1}{2}x \)Если уравнение имеет более одного корня, в ответе запишите больший из корней.
Смотреть решение
6. Четырёхугольник АВСD вписан в окружность. Угол АBС равен 106°, угол САD равен 69°. Найдите угол АВD. Ответ дайте в градусах.
Смотреть решение
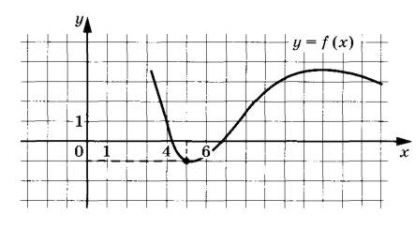
7. На рисунке изображён график функции у = f(х). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 5. Найдите значение производной функции в точке х0 = 5.
Смотреть решение
8. В прямоугольном параллелепипеде АВСDА1В1C1D1 известно, что АВ = 9‚ ВС = 6‚ АА1 = 5. Найдите объём многогранника, вершинами которого являются точки А, В, С, D, А1, В1.
Смотреть решение
9. Найдите значение выражения соs α, если \( tga=-\frac{\sqrt{21}}{2} \) и \( \frac{3\pi}{2}<=a<=2 \pi \)
Смотреть решение
10. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением p1·V11,4 = p2·V21,4‚ где р1 и р2 – давление газа (в атмосферах) в начальном и конечном состояниях, V1 и V2 – объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 192 л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало 128 атмосфер? Ответ дайте в литрах.
Смотреть решение
11. Две трубы, работая одновременно, наполняют бассейн за 18 часов 40 минут, а одна первая труба наполняет бассейн за 40 часов. За сколько часов наполняет бассейн одна вторая труба?
Смотреть решение
12. Найдите точку максимума функции \( y=-\frac{x^2+196}{x} \)