1. Решите уравнение \( 3log_{8}(x-2)=log_{2}\sqrt{2x-1} \) Если уравнение имеет более одного корня, в ответ запишите меньший из них.
Смотреть решение
2. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Смотреть решение
3. В треугольнике АВС сторона АВ равна 10, угол А‐острый. Найдите медиану ВМ, если АС=20, а площадь треугольника АВС равна 96.
Смотреть решение
![]()
Смотреть решение
5. Гранью параллелепипеда является ромб со стороной 1 и острым углом 45°. Одно из рёбер параллелепипеда составляет с плоскостью этой грани угол 45° и равно 7. Найдите объём параллелепипеда.
Смотреть решение
6. Функция y=f(x) определена на промежутке (—3;7). На рисунке изображён график её производной y=f'(x) Найдите число касательных к графику функции y=f(x), которые наклонены под углом 150° к положительному направлению оси абсцисс.
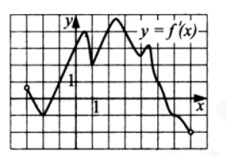
Смотреть решение
7. Автомобиль, масса которого равна =2160 кг, начинает двигаться с ускорением, которое в течение t секунд остается неизменным, и проходит за это время путь S =500 метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно \( F=\frac{2mS}{t^2} \) Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила F, приложенная к автомобилю, не меньше 2400 Н. Ответ выразите в секундах.
Смотреть решение
8. Два станка одновременно начали штамповать детали с производительностью 70 деталей в минуту каждый. Через час пустили в работу третий станок. В этот момент первый станок снизил свою производительность на 10 деталей в минуту. Через некоторое время на третьем станке было сделано столько деталей, сколько было к этому моменту на первом, а еще через 3,5 часа он сравнялся по числу сделанных деталей со вторым. Найти производительность работы третьего станка (в деталях в минуту).
Смотреть решение
9. На рисунке изображены графики функций \( f(x)=5x+9 \) и \( g(x)=ax^2+bx+c \) которые пересекаются в точках А и В. Найдите абсциссу точки В.
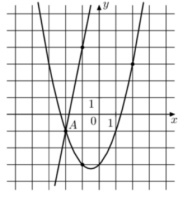
Смотреть решение
10. Маша коллекционирует принцесс из Киндер‐сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом очередном Киндер‐сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши уже есть две разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придётся купить ещё 2 или 3 шоколадных яйца?
Смотреть решение
11. Найдите наименьшее значение функции \( y=6x-3sinx-5\pi \) на отрезке \( [\frac{5\pi}{6};\frac{3\pi}{2}] \)
Смотреть решение
