1. Решите уравнение \( (x^2-9)(\sqrt{3-2x}-x)=0 \)Если уравнение имеет более одного корня, в ответе укажите больший из них.
Смотреть решение
2. В группе шесть человек, среди них – Михаил и Олег. Группу случайным образом делят на 3 пары. Найти вероятность того, что Михаил и Олег окажутся в одной паре.
Смотреть решение
3. В ромб ABCD вписана окружность, касающаяся стороны AD в точке F. Известно, что AF =4 ∙ FD. Найдите косинус острого угла ромба.
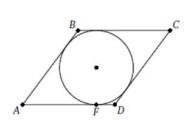
Смотреть решение
4. Найдите значение выражения \( \frac{5sin98°}{sin49°*sin41°} \)
Смотреть решение
5. На рисунке изображен многогранник, все двугранные углы которого прямые. Найдите квадрат расстояния между вершинами А и С3.
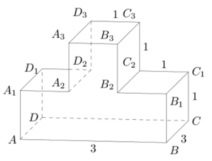
Смотреть решение
6. На рисунке изображен график функции y=f(x) . На оси абсцисс отмечены точки ‐2, ‐1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
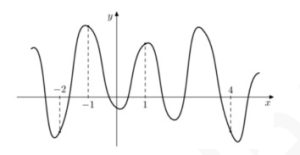
Смотреть решение
7. Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону \( U=U_{0}cos(wt+\phi) \)где t ‐ время в секундах, амплитуда U0 = 2 В, частота \( w=240° \), а фаза \( \phi=-120° \). Датчик настроен так, что если напряжение в нем не ниже, чем 1 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
Смотреть решение
8. Из пункта А в пункт В вышел грибник, через час из А в В вышел турист, скорость которого на 25% больше скорости грибника, а еще через час после этого из А в Ввышел спортсмен, скорость которого на 60% больше скорости туриста. Грибник и турист прибыли в пункт В одновременно. На сколько минут раньше прибыл в пункт В спортсмен?
Смотреть решение
9. На рисунке изображены графики функций \( f(x)=a\sqrt{x} \) и \( g(x)=kx+b \) которые пересекаются в точке А. Найдите ординату точки А
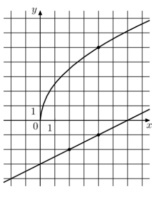
Смотреть решение
10. Турнир по настольному теннису проводится по олимпийской системе: игроки случайным образом разбиваются на игровые пары; проигравший в каждой паре выбывает из турнира, а победитель выходит в следующий тур, где встречается со следующим противником, который определен жребием. Всего в турнире 16 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга – Иван и Алексей. Какова вероятность того, что этим двоим в каком‐то туре придется сыграть друг с другом?
Смотреть решение
11. Найти наибольшее значение функции \( y=\frac{2}{\sqrt{x^2+2x+5}} \) на промежутке [-2;2]
Смотреть решение
