1. Решите уравнение \( x^2-\sqrt{(x-1)^2}=1 \). Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Смотреть решение
2. Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.
Смотреть решение
3. Точки M и N лежат на окружности и делят её на две дуги, одна из которых втрое короче другой. Известно, что MN=5. Найдите площадь S круга, ограниченного данной окружностью. В ответе укажите число \( \frac{S}{\pi} \)
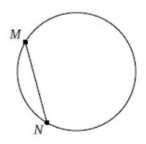
Смотреть решение
4. Найдите значение выражения
\( log_{2}\sqrt{\sqrt{3}-1}+log_{4}(1+\sqrt{3}) \)
Смотреть решение
5. В цилиндр вписана сфера. Площадь полной поверхности цилиндра равна 42. Найдите площадь поверхности сферы.
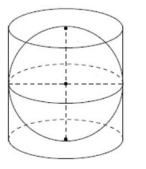
Смотреть решение
6. На рисунке изображен график производной функции \( f(x) \)определенной на интервале (−1; 13). Найдите промежутки возрастания функции f(x) . В ответе укажите сумму целых чисел, входящих в эти промежутки.

Смотреть решение
7. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 40 см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 до 60 см, а расстояние d2 от линзы до экрана – в пределах от 180 до 200 см. Изображение на экране будет четким, если выполнено соотношение \( \frac{1}{d_{1}}+\frac{1}{d_{2}}=\frac{1}{f} \)Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было чётким. Ответ выразите в сантиметрах.
Смотреть решение
8. Проценты содержания спирта (по весу) в трех растворах образуют геометрическую прогрессию. Если смешать первый, второй и третий растворы в весовом отношении 2:3:4, то получится раствор, содержащий 32% спирта. Если же смешать их в весовом отношении 3:2:1, то получится раствор, содержащий 22% спирта. Сколько процентов спирта содержит первый раствор?
Смотреть решение
9. На рисунке изображены графики функций \( f(x)=4x^2-25x+41 \) и \( g(x)=ax^2+bx+c \)которые пересекаются в точках А и В. Найдите ординату точки В.
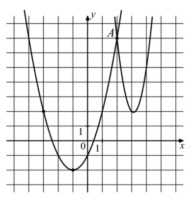
Смотреть решение
10. Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью р = 0,8 на единицу больше предыдущего и с вероятностью 1 – р на единицу меньше предыдущего. Какова вероятность того, что какой‐то член этой последовательности окажется равен – 1?
Смотреть решение
11. Найдите точку минимума функции \( f(x)=\frac{x^3+4}{x^2} \)
Смотреть решение
