1. Решите уравнение \( \frac{3^{x^2}-81}{x-2}=0 \) Если уравнение имеет более одного корня, в ответе укажите больший из них.
Смотреть решение
2. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,03. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Смотреть решение
3. Окружность, вписанная в треугольник ABC, касается его стороны BC в точке N. Известно, что BN =15 и AC =17. Найдите периметр треугольника.

Смотреть решение
4. Найдите значение выражения \( \frac{9^{x+11}*2^{3x+8}}{3^{2x+11}*4^{x+4}} \) при \( x=2 \)
Смотреть решение
5. Основанием наклонной призмы ABCD A1B1C1D1 является квадрат ABCD, а диагональ AC1 призмы перпендикулярна плоскости основания. Найдите площадь основания призмы, если \( AC_{1}=2\sqrt{7} \), \( AA_{1}=6 \)
Смотреть решение
6. На рисунке изображен график \( y=f'(x) \)— производной функции \( f(x) \) определенной на интервале (‐5; 19). Найдите количество точек максимума функции \( f(x) \) , принадлежащих отрезку [‐3; 15].
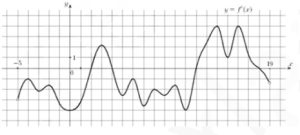
Смотреть решение
7. Скорость колеблющегося на пружине груза меняется по закону \( v(t)=3*sin\frac{\pi t}{4} \) (см/с), где t — время в секундах. Какую долю времени из первой\ секунды скорость движения превышала 1,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Смотреть решение
8. Аркадий продал партию компьютеров, а Борис продал партию принтеров, и их выручка оказалась одинаковой. «Если бы принтер стоил столько же, сколько компьютер, я бы получил 192 млн. рублей» ‐ сказал Борис. «Если бы компьютер стоил столько же, сколько принтер, я бы получил 75 млн. рублей» ‐ ответил Аркадий. На сколько процентов компьютер дороже принтера?
Смотреть решение
9. На рисунке изображен график функции \( f(x)=atgx+b \). Найдите b .
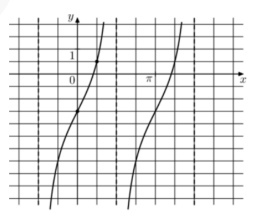
Смотреть решение
10. В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш‐беш»: гость бросает одновременно 2 игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.
Смотреть решение
11. Найдите наибольшее значение функции \( y+6=12sinx-6\sqrt{3}x+\sqrt{3}\pi+6 \) отрезке [0;pi/2]
Смотреть решение
