1. Решите уравнение \( 5^{x^2-3}*6^x=180 \). В ответе укажите наибольший корень этого уравнения.
Смотреть решение
2. Пятеро друзей‐автолюбителей взяли автомобиль в аренду для путешествия. С помощью жребия они выбирают двоих, которые в первый день будут поочередно водителями. Какова вероятность того, что М., входящий в состав группы, будет водителем в первый день путешествия?
Смотреть решение
3. В треугольнике АВС угол С равен 90, \( cos∠B=\frac{\sqrt{51}}{10} \). Найдите синус внешнего угла при вершине В.
Смотреть решение
4. Найдите значение выражения \( \frac{sin^220+sin^270}{2sin(180+\alpha)} \), если \( sin\alpha=\frac{1}{3} \)
Смотреть решение
5. Сосуд в виде правильной треугольной пирамиды высотой \( 25\sqrt{3} \)см доверху заполнен водой. Найдите, на какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, имеющий форму куба со стороной, равной стороне основания данной треугольной пирамиды. Ответ выразите в сантиметрах
Смотреть решение
6. Функция у = f(x) определена на промежутке (‐ 4; 4). На рисунке изображен ее график и касательная к этому графику в точке с абсциссой \( x_{0}=-3 \) Вычислите значение производной функции \( y=\frac{x}{4}f(x)+5x \) в точке \( x_{0}=-3 \)
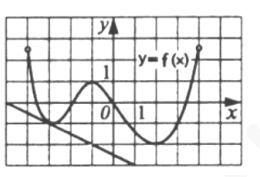
Смотреть решение
7. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объeм и давление связаны соотношением \( pV^{1,2}=const \)где p (атм.) — давление в газе, V — объeм газа в литрах. Изначально объeм газа равен 51,2 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 64 атмосфер. Определите, до какого минимального объёма можно сжать газ. Ответ выразите в литрах.
Смотреть решение
8. Экипаж дальнобойщиков проехал расстояние 6375 км с определенной скоростью без остановок. На обратном пути водители планируют сделать остановку на 10 часов для отдыха. Для этого на обратном пути им необходимо увеличить скорость на 10 км/ч по сравнению с прямым маршрутом. Найдите (в км/ч) значение первоначальной скорости, если на путь в обоих направлениях затрачено одинаковое количество времени.
Смотреть решение
9. На рисунке изображен график функции \( f(x)=asinx+b \). Найдите \( a \)
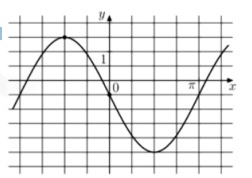
Смотреть решение
10. Артем бросил одновременно две игральных кости, ни на одной из них не выпало шесть. Какова вероятность при этом условии, что в сумме выпало 9 очков?
Смотреть решение
11. Найдите наибольшее значение функции \( y=\frac{15\sqrt{3}}{\pi}+\frac{3}{\pi}(24x-5tgx) \) на отрезке [\( -\frac{\pi}{6};\frac{\pi}{3} \)]
Смотреть решение
