1. Решите уравнение \( 11^{79}*(\frac{1}{11})^x*(\frac{1}{11})^{\sqrt{x+1}}=1 \)
Смотреть решение
2. Найдите вероятность того, что случайно выбранное трехзначное число делится на 34.
Смотреть решение
3. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 4 : 7 : 9. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 338.
Смотреть решение
4. Вычислите \( sin555°*sin1185°*tg405° \)
Смотреть решение
5. В основании пирамиды лежит прямоугольник. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы 30° и 45°. Найдите диагональ прямоугольника, если высота пирамиды равна 4.
Смотреть решение
6. На рисунке изображены участки графика функции y=f(x) и касательной к нему в точке с абсциссой x=0 . Известно, что данная касательная параллельна прямой, проходящей через точки графика с абсциссами x =-2 и x = 2 . Используя это, найдите значение производной f'(0)
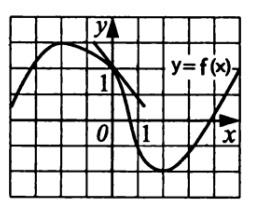
Смотреть решение
7. Автомобиль, масса которого равна = 1200 кг, начинает двигаться с ускорением, которое в течение t секунд остается неизменным, и проходит за это время путь S=300 метров. Значение силы (в ньютонах), приложенное в это время к автомобилю, можно вычислить по формуле по формуле \( F=\frac{2mS}{t^2} \).Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила F , приложенная к автомобилю, не меньше 1800 Н. Ответ выразите в секундах.
Смотреть решение
8. Готовясь к олимпиаде по математике, школьник за 10 недель прорешал 700 задач. Приобретая опыт, он в каждую последующую неделю, начиная со второй, решал на 10 задач больше, чем в предыдущую. Какое количество задач успеет прорешать школьник за остающиеся до олимпиады 4 недели, если будет увеличивать количество еженедельно решаемых задач прежним образом?
Смотреть решение
9. На рисунке изображен график функции \( f(x)=a^x+b \). Найдите \( f(6) \)
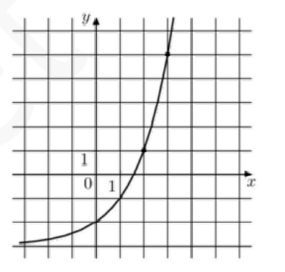
Смотреть решение
10. Васе нужно забить в дубовую доску гвоздь. Если гвоздь стальной, то он согнется с вероятностью 0,1, а если гвоздь медный, то он согнется с вероятностью 0,3. На столе вперемешку лежат 6 стальных и 4 медных гвоздя. Вася берет первый попавшийся гвоздь со стола и пытается забить его в доску. Найдите вероятность того, что этот гвоздь не согнется.
Смотреть решение
11. Найдите наибольшее значение функции \( y=\frac{3x-\pi}{\pi}cosx-\frac{3}{\pi}sinx+21 \)на отрезке [0;2pi]
Смотреть решение
