1. Решите уравнение \( \sqrt{x^2+6x+8}=\sqrt{x+2} \) . Если уравнение имеет более одного корня, в ответе запишите меньший из них
Смотреть решение
2. В коробке 10 синих, 9 красных и 6 зеленых фломастеров. Случайным образом выбирают 2 фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
Смотреть решение
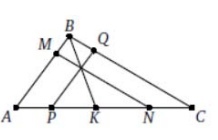
3. На сторонах AB и BC треугольника ABC выбраны соответственно точки M и Q, а на стороне AC —точки P, K, N (именно в таком порядке, считая от A) таким образом, что MN || BC, PQ || AB и KB проходит через точку пересечения MN и PQ. Известно, что AP =4, PK =5 и KN =6. Найдите NC
Смотреть решение
4. Найдите значение выражения \( -\frac{22}{cos^234°+cos^2124°} \)
Смотреть решение
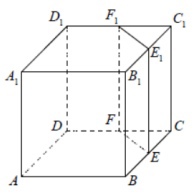
5. Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 25. Найдите объём куба.
Смотреть решение
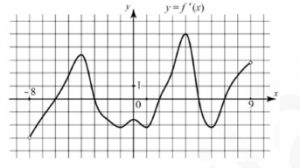
6. На рисунке изображён график производной \( y=f'(x) \)функции f(x), определённой на интервале (‐8; 9). Найдите количество точек минимума функции f(x) , принадлежащих отрезку [‐2; 8]
Смотреть решение
7. Автомобиль, движущийся в начальный момент времени со скоростью V0=17 м/с, начал торможение с постоянным ускорением a = 2 м/с2. За t секунд после начала торможения он прошёл путь \( S=V_{0}t-\frac{at^2}{2} \) .Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 60 метров. Ответ выразите в секундах.
Смотреть решение
8. Из пункта А круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через полчаса после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Смотреть решение
9. На рисунке изображен график функции \( f(x)=\frac{kx+a}{x+b} \)Найдите k .

Смотреть решение
10. При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР‐тест. Если заболевание действительно есть, то тест подтверждает его в 86 % случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев.
Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР‐тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?
Смотреть решение
11. Найдите наибольшее значение функции y=15+12x-x^3 на отрезке [-2;2]
Смотреть решение
