1. Решите уравнение \( 2^{x^2-3}*5^{x^2-3}=0,01*(10^{x-1})^3 \)
В ответе запишите сумму всех корней уравнения.
Смотреть решение
2. Игральный кубик бросают дважды. Найдите вероятность того, что сумма выпавших
очков будет меньше, чем 4. Ответ округлите до сотых.
Смотреть решение
3. Радиус окружности, вписанной в прямоугольный треугольник, равен 6. Найдите гипотенузу, если точка касания с вписанной окружностью делит ее на отрезки, длины которых относятся как 5 : 12.
Смотреть решение
4. Вычислите \( log_{16}a-log_{16}b \), если \( a-4b=0 \)
Смотреть решение
5. В правильной треугольной пирамиде боковое ребро равно 15, а тангенс угла между боковой гранью и плоскостью основания равен \( \sqrt{23} \)Найдите сторону
основания пирамиды
Смотреть решение
6. К графику функции проведена y=f(x) касательная в точке с абсциссой x0=3 . Определите градусную меру угла наклона касательной, если на рисунке изображен график производной этой функции
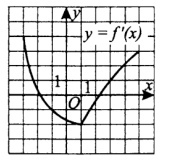
Смотреть решение
7. Глубоководники проектируют новый батискаф в виде сферы радиуса R. Выталкивающая сила Архимеда, действующая на батискаф, вычисляется по
формуле \( F_{A}=ρgV=ρg\frac{4}{3} \pi R^3 \) Определите максимальный радиус батискафа (в метрах), если сила Архимеда по технологии не должна превосходить 1130400 Н. При расчёте примите следующие значения постоянных: \( ρ=1000 \) кг/м^3; g=10 Н/кг; pi =3,14.
Смотреть решение
8. В бутыли содержится 25 %‐ый раствор соли. Из нее вылили некоторую часть раствора и добавили такое же количество воды. В результате получили 12 %‐ый раствор соли. Какая часть первоначального раствора была заменена водой?
Смотреть решение
9. На рисунке изображен график функции вида \( f(x)=b+log_{a}x \). Найдите\( f(32) \)
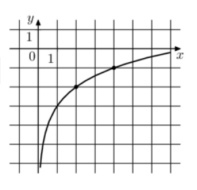
Смотреть решение
10. В бутике модной обуви в случайный момент каждый продавец занят с покупателем с вероятностью 0,1. Всего продавцов трое. Найдите вероятность того, что в случайно выбранный момент хотя бы один из продавцов свободен.
Смотреть решение
11. Найдите наименьшее значение функции \( y=\frac{5x^2+2}{3x^2+20}+\frac{3x^2+20}{5x^2+2} \)на отрезке [-1;4]
Смотреть решение
