1. Решите уравнение \( 4^x-4^{2-x}-15=0 \) Если корней несколько, то в ответе укажите их произведение.
Смотреть решение
2. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Смотреть решение
3. В треугольнике ABC известно, что ∠ABC=74 Биссектрисы AK и CN этого треугольника пересекаются в точке O Найдите ∠AOC . Ответ дайте в градусах
Смотреть решение
4. Найдите значение выражения \( \sqrt{11-x-4\sqrt{7-x}}+\sqrt{6-x-6\sqrt{7-x}} \) при \( x=2 \)
Смотреть решение
5. В цилиндрический сосуд налили 2000 см3 воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
Смотреть решение
6. На рисунке изображен график функции f(x) Касательная к этому графику, проведенная в точке с абсциссой 4, проходит через начало координат. Найдите f'(4).
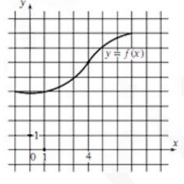
Смотреть решение
7. Высота над землёй подброшенного вверх мяча меняется по закону \( h(t)=1,4+14t-5t^2 \)где – высота в метрах, – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 8 метров?
Смотреть решение
8. Из города A в город B одновременно выехали два автомобиля: первый со скоростью 65 км/ч, а второй—со скоростью 60 км/ч. Через 24 минуты следом за ними выехал третий автомобиль. Найдите скорость третьего автомобиля, если известно, что с момента, когда он догнал второй автомобиль, до момента, когда он догнал первый автомобиль, прошло 40 минут. Ответ дайте в км/ч.
Смотреть решение
9. На рисунке изображен график функции f(x)=kx+b Найдите f(-5).
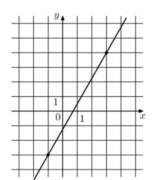
Смотреть решение
10. В ящике 4 красных и 2 синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?
Смотреть решение
11. Найдите наименьшее значение функции \( y=\frac{x^2-6x+36}{x} \)на отрезке [3;9]
Смотреть решение
