1. Больному прописан курс лекарства, которое нужно принимать по 0,5 г 2 раза в день в течение 21 дня. Упаковка содержит 10 таблеток по 0,5 г. Какое наименьшее количество упаковок требуется на весь курс лечения?
Смотреть решение
2. На рисунке показано, как изменялась температура воздуха с 3 по 5 апреля. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия.
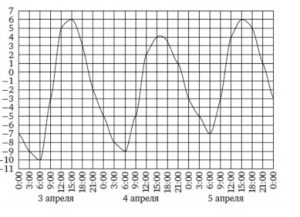
Найдите разность между наименьшим и наибольшим значениями температуры в первой половине суток 5 апреля. Ответ дайте в градусах Цельсия
Смотреть решение
3. На клетчатой бумаге со стороной клетки 1 изображена фигура. Найдите площадь закрашенной её части.
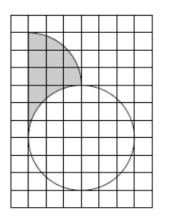
Смотреть решение
4. При контроле качества мебельных щитов на деревообрабатывающем комбинате 31% щитов определяется во второй сорт, 5% щитов отбраковывается. Остальные щиты продаются как первый сорт. Найдите вероятность того, что случайно выбранный новый щит окажется первого сорта. Ответ округлите до сотых.
Смотреть решение
5. Решите уравнение \( 4^{lgx}-32+x^{lg4}=0 \)
Смотреть решение
6. Дан треугольник ABC площади 1. На продолжении его стороны AB за точку B выбрана точка K так, что AB = BK. На продолжении BC за точку C выбрана точка L так, что BC =CL, а на продолжении CA за точку A—точка M так, что CA= AM. Найдите площадь треугольника KLM.
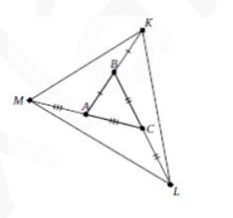
Смотреть решение
7. Материальная точка движется прямолинейно по закону \( x(t)=t^3-t^2-12t+18 \)(где x — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения). В какой момент времени ее скорость была равна 9 м/с?
Смотреть решение
8. Сосуд, имеющий форму полусферы, заполнен водой. Какое наименьшее число одинаковых стаканов, имеющих форму цилиндра, радиус которого в 3 раза меньше радиуса полусферы, а высота в два раза больше радиуса полусферы, потребуется для того, чтобы перелить всю эту воду?
Смотреть решение
9. Найдите значение выражения \( g(x-6)*g(6,5-x) \), если \( g(x)=36^x \)
Смотреть решение
10. Если достаточно быстро вращать ведёрко с водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведёрка сила давления воды на дно не остаётся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила её давления на дно будет положительной во всех точках траектории, кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна \( P=m*(\frac{v^2}{L}-g) \)где m —масса воды в килограммах, v —скорость движения ведёрка в м/с, L — длина верёвки в метрах, g — ускорение свободного падения (считайте, что g =10 м/с2). С какой минимальной скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 0,625 м? Ответ выразите в м/с.
Смотреть решение
11. Ваня сбежал вниз по движущемуся эскалатору и насчитал 40 ступенек. Затем он пробежал вверх по тому же эскалатору с той же скоростью относительно эскалатора и насчитал 60 ступенек. Сколько ступенек он насчитал бы, спустившись по неподвижному эскалатору?
Смотреть решение
12. Найдите наименьшее значение функции \( y=2x-2*ln(x+3)+3 \) на отрезке [-2,5;1]
Смотреть решение
