1. 8 рабочих выполнили работу за 6 дней. За сколько дней выполнили бы ту же работу 12 рабочих при той же производительности труда?
Смотреть решение
2. На диаграмме показаны средние цены в интернет‐магазинах на пылесосы модели А и модели Б в период с мая по декабрь 2019 года. По горизонтали указаны месяцы, по вертикали – цены (в рублях). По диаграмме определите, сколько месяцев с мая по декабрь 2019 года средняя цена пылесоса модели Б была выше средней цены пылесоса модели А
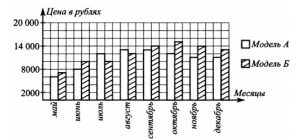
Смотреть решение
3. На клетчатой бумаге изображен с размером клетки 1 см х 1 см изображен треугольник. Найдите его площадь. Ответ дайте в квадратных сантиметрах.
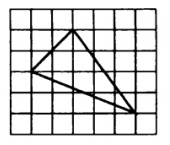
Смотреть решение
4. Найдите вероятность того, что случайно выбранное трехзначное число делится на 4.
Смотреть решение
5. Решите уравнение: \( 4x^4-11x^2-9x-2=0 \) Если уравнение имеет несколько корней, в ответе укажите наибольший корень.
Смотреть решение
6. Даны треугольник АВС, в котором АВ=ВС=25, АС = 30, и окружность с центром в точке В радиуса 15. Вторая окружность проходит через точки А и С и касается первой внешним образом. Найдите радиус второй окружности.
Смотреть решение
7. Прямая у=2х является касательной к графику функции \( y=7x^2+bx+5\frac{1}{7} \). Найдите b, учитывая, что абсцисса точки касания больше 0.
Смотреть решение
8. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 5, а боковые ребра равны 7 и наклонены к плоскости основания под углом 60.
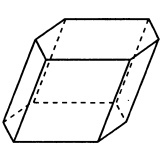
Смотреть решение
9. Вычислить:
\( cos\frac{\pi}{33}cos\frac{2\pi}{33}cos\frac{4\pi}{33}cos\frac{8\pi}{33}cos\frac{16\pi}{33} \)
Смотреть решение
10. Скорость колеблющегося на пружине груза меняется по закону \( v(t)=3,2sin \pi t \)(см/с), где t – время в секундах. Какую долю времени из первой секунды скорость движения превышала 1,6 см/с? Ответ выразите десятичной дробью, округлив до сотых.
Смотреть решение
11. На участке реки от А до В течение так невелико, что им можно пренебречь; на участке от В до С течение оказывает заметное влияние на движение лодки. Лодка покрывает расстояние вниз от А до С за 6 ч, а вверх от С до А за 7 ч. Если бы на участке от А до В течение было бы таким же, как на участке от В до С, то весь путь от А до С занял бы 5,5 ч. Сколько часов в этом случае понадобилось бы той же лодке на движение вверх от С до А? Собственная скорость лодки принимается неизменной во всех случаях.
Смотреть решение
12. Найдите наименьшее значение функции
\( y=\frac{4}{\sqrt{x^2+16}} \) на отрезке [-3;3]
Смотреть решение
