1. На пошив 6 палаток нужно 120 м брезента шириной 1,2 м. Сколько метров брезента шириной в 1,5 м надо на пошив 4 таких палаток?
Смотреть решение
2. На рисунке жирными точками показано суточное количество осадков, выпавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее количество осадков выпало в период с 13 по 20 января. Ответ дайте в миллиметрах.
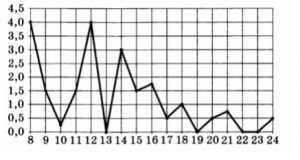
Смотреть решение
3. На клетчатой бумаге изображен круг. Какова площадь круга, если площадь заштрихованного сектора равна 27?

Смотреть решение
4. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором и третьем справочниках, равна соответственно 0,6, 0,7 и 0,8. Найдите вероятность того, что формула содежится не менее чем в двух справочниках. Ответ округлите до сотых.
Смотреть решение
5. Решите уравнение: \( \frac{\sqrt{27+x}+\sqrt{27-x}}{\sqrt{27+x}-\sqrt{27-x}}=\frac{27}{x} \)Если уравнение имеет несколько корней, в ответе укажите наименьший корень.
Смотреть решение
6. Три стороны четырехугольника, взятые в последовательном порядке, равны соответственно 10, 3 и 8 см. Известно, что в этот четырехугольник можно вписать окружность и около него можно описать окружность. Найдите площадь четырехугольника.
Смотреть решение
7. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0 Найдите значение производной функции f(x) в точке x0.
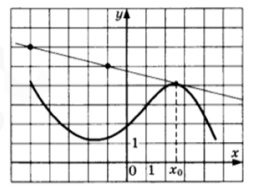
Смотреть решение
8. Объем треугольной пирамиды равен 135. Точки пересечения медиан всех ее граней являются вершинами второй пирамиды. Найдите ее объем.
Смотреть решение
9. Вычислить: \( \frac{3log_{3}15*log_{5}9-2log_{5}^215-log_{5}^29}{log_{5}9-log_{5}15} \)
Смотреть решение
10. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объем и давление связаны соотношением \( pV^{1,4}=const \)где р (атм.) – давление газа, V – объем газа в литрах. Изначально объем газа равен 24 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 128 атмосфер. Определите, до какого минимального объема можно сжать газ. Ответ выразите в литрах.
Смотреть решение
11. Два автомобиля выехали одновременно из одного пункта в одном и том же направлении. Один автомобиль идет со скоростью 50 км/ч, а другой 40 км/ч. Спустя полчаса из того же пункта в том же направлении выехал третий автомобиль, который обогнал первый автомобиль на 1,5 часа позже, чем второй. Найдите скорость третьего автомобиля в км/час.
Смотреть решение
12. Найдите наименьшее значение функции \( y=\frac{sin2x}{sin(x+\frac{\pi}{4})} \) на отрезке [0;pi/2]
Смотреть решение
