1. Цена на автомобиль престижной марки ежегодно увеличивается на одно и то же число процентов по сравнению с предыдущим годом. На сколько процентов каждый год увеличивалась цена автомобиля, если, выставленный на продажу за 2560000 рублей, он через два года был продан за 4000000 рублей?
Смотреть решение
2. При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси – напряжение в вольтах. Определите по графику за сколько часов работы фонарика напряжение упадет с 1,6 В до 0,8 В.
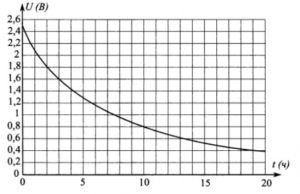
Смотреть решение
3. Найдите площадь закрашенной фигуры, изображённой на клетчатой бумаге со стороной клетки 1 см. Ответ выразите в квадратных сантиметрах.
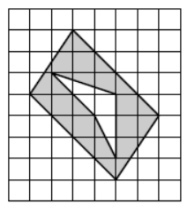
Смотреть решение
4. Участник Б выходит в финал только если он справится со своим заданием, а участник А при этом не справится со своим заданием. Когда у участника А оставалась одна попытка, а у участника Б – две, вероятность выхода Б в финал равнялась 0,32. Когда он неудачно истратил одну свою попытку, вероятность снизилась до 0,2. Чему она будет равна, если участник А после этого тоже выступит неудачно? (Автор задачи Николай Журавлев)
Смотреть решение
5. Решите уравнение: \( (x+\frac{1}{x})^2-4,5*(x+\frac{1}{x})+5=0 \) Если корней несколько, в ответе укажите их произведение.
Смотреть решение
6. Высота BH ромба ABCD делит его сторону AD на отрезки AH =1 и HD=8. Найдите BD.

Смотреть решение
7. Прямая \( y=-4x+15 \)является касательной к графику функции \( y=x^3-6x^2+8x+7 \)Найдите абсциссу точки касания.
Смотреть решение
8. В правильной шестиугольной пирамиде сторона основания равна 1, а апофема равна √3. Найдите угол между боковой гранью и основанием. Ответ дайте в градусах.
Смотреть решение
9. Найдите значение выражения \( \frac{lg5}{lg(10log_{2}(4\sqrt{2}))} \)
Смотреть решение
10. В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в
нём, выраженная в метрах, меняется по закону
\( H(t)=H_{0}-\sqrt{2gH}kt+\frac{g}{2}k^2t^2 \) где ‐ время (в секундах), прошедшее с момента открытия крана, \( H_{0}=20 \) м ‐
начальная высота столба воды, \( k=\frac{1}{400} \)‐ отношение площадей поперечных сечений крана и бака, g ‐ускорение свободного падения (считайте, что g = 10 м/с2). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма?
Смотреть решение
11. Из городов A и B навстречу друг другу одновременно выехали с постоянными скоростями два автомобиля. Скорость первого автомобиля была в два раза больше скорости второго. Второй автомобиль прибыл в A на 1 час позже, чем первый прибыл в B. На сколько минут раньше произошла бы встреча автомобилей, если бы второй автомобиль ехал с той же скоростью, что и первый?
Смотреть решение
12. Найдите наименьшее значение функции \( y=\frac{7}{\pi}x-\frac{4}{3}cosx-3 \) на отрезке [\( -\frac{2 \pi}{3};-\frac{\pi}{2} \)]
Смотреть решение
