1. Если Сергей купит 15 тетрадей, то у него останется 7 рублей, если же он купит 20 тетрадей, то ему не хватит 8 руб. Сколько денег у Сергея? Ответ дайте в рублях.
Смотреть решение
2. Грузовая машина отправилась из магазина на склад, где провела некоторое время в процессе погрузки, и вернулась обратно по тому же самому маршруту. На рисунке изображен график движения этой машины: по оси абсцисс откладывается время (в минутах) с момента выезда машины от магазина, по оси ординат – расстояние от машины до магазина (в км, вдоль маршрута движения). Найдите по графику скорость машины при движении на склад. Ответ выразите в км/ч.
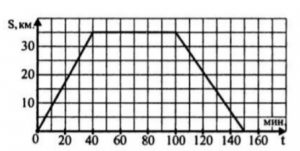
Смореть решение
3. Какой наименьший радиус может иметь окружность с центром в точке А(‐ 9; ‐ 6), если она касается окружности радиуса 1 с центром в точке В(15; 12)?
Смотреть решение
4. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная. Ответ округлите до сотых.
Смотреть решение
5. Решите уравнение:
\( x^5+\frac{1}{x^5}=\frac{205}{16}(x+\frac{1}{x}) \)
Если уравнение имеет несколько корней, в ответе укажите наименьший корень.
Смотреть решение
6. Площадь равнобедренной трапеции равна 180 см2. Найдите длину верхнего основания, если боковые стороны равны по 13 см, а нижнее основание 20 см. Ответ дайте в см.
Смотреть решение
7. Функция y=f(x) определена на промежутке (‐5;6). На рисунке изображен график ее производной. Найдите точку, в которой функция y=f(x) принимает наименьшее значение.
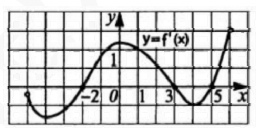
Смотреть решение
8. Точка, лежащая на окружности верхнего основания цилиндра, соединена с точкой, лежащей на окружности нижнего основания. Угол между проведенной прямой и осью цилиндра составляет 45. Найдите радиус цилиндра, если длина отрезка, соединяющего выбранные точки, равна 7√2, а радиус цилиндра равен его высоте.
Смотреть решение
9. Вычислить: \( sin(actg\frac{8}{15}-arccos\frac{15}{17}) \)
Смотреть решение
10. Уравнение процесса, в котором участвовал газ, записывается в виде \( PV^\alpha=const \)где P (Па) — давление в газе, V — объем газа в кубических метрах, a — положительная константа. При каком наименьшем значении константы a уменьшение объёма газа в 16 раз приводит к увеличению давления не менее, чем в 32 раза?
Смотреть решение
11. Дорога проходит через пункты А и В. Велосипедист выехал из А по направлению к В. Одновременно с ним из пункта В вышли с равными скоростями два пешехода: первый в пункт А, а второй – в противоположном направлении. Велосипедист проехал от А до В за 0,5 ч и, продолжая движение, догнал второго пешехода. Это произошло через 1,2 ч после встречи велосипедиста с первым пешеходом. Определить время (в часах) движения велосипедиста от начала движения до встречи с первым пешеходом?
Смотреть решение
12. Найдите наименьшее значение функции \( y=5x^3-x|x+1| \)на отрезке [-2;0]
Смотреть решение
