1. Школьный портфель стоил 6000 рублей. Через некоторое время цену увеличили на 10%, а затем уменьшили на 10%. Какой стала цена портфеля? Ответ дайте в рублях.
Смотреть решение
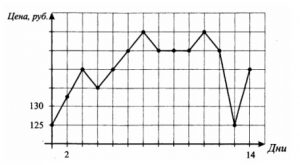
2. На графике, изображенном на рисунке, жирными точками показано изменение биржевой стоимости акций компании в первые две недели июля. По оси абсцисс отложены числа месяца, по оси ординат – стоимость одной акции в рублях. Для наглядности жирные точки соединены линией. 3 июля бизнесмен приобрел 200 акций этой компании. 50 из них он продал 4 июля, а 13 июля – остальные 150. Сколько рублей потерял бизнесмен в результате этих операций?
Смотреть решение
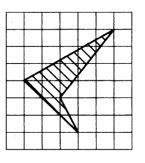
3. На клетчатой бумаге с размером клеток 1см х 1см изображен четырехугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
Смотреть решение
4. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе – 0,9, в третье – 0,8. Найдите вероятность того, что только одно отделение получит газеты вовремя.
Смотреть решение
5. Решите уравнение: \( 27^x-8^x=3(18^x-12^x) \)
Смотреть решение
6. На основании равнобедренного треугольника построен правильный треугольник, площадь которого в 3 раза больше площади данного. Найдите наибольший угол исходного треугольника. Ответ дайте в градусах.
Смотреть решение
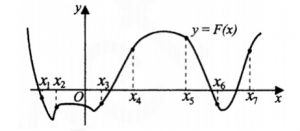
7. На рисунке изображен график функции y=F(x), где F(x)- первообразная функции y=f(x) Найдите среди точек x1, x2, x3, x4, x5, x6, x7 те, в которых функция f(x) положительна. В ответе запишите количество найденных точек.
Смотреть решение
8. В основании пирамиды лежит параллелограмм. Высота пирамиды проходит через точку пересечения диагоналей параллелограмма. Большее боковое ребро образует с плоскостью основания угол 60° и равно \( 6\sqrt{3} \). Найдите высоту пирамиды.
Смотреть решение
9. Найдите значение выражения
\( 2\sqrt{3}\frac{sin50°*sin100°+cos50°*sin10°}{cos40°*cos100°+sin40°*cos10°} \)
Смотреть решение
10. Парашютисты‐экстремалы определяют высоту сооружений для будущих прыжков, засекая время падения небольших камней с вершин сооружений до поверхности приземления. Приближенная зависимость высоты от времени свободного падения имеет вид \( р=4,9t^2 \). Здесь h – высота в метрах, t – время в секундах. С вершины первого сооружения камень падал 4,5 с. На сколько метров второе сооружение выше первого, если с вершины второго сооружения камень падал на 1 с дольше?
Смотреть решение
11. Две бригады должны были закончить уборку урожая за 12 дней. После 8 дней совместной работы первая бригада получила другое задание, поэтому вторая бригада закончила оставшуюся часть работы за 7 дней. На сколько дней вторая бригада убрала бы весь урожай быстрее первой, если бы каждая бригада работала отдельно?
Смотреть решение
12. Найдите точку минимума функции \( y=\frac{5^{log_{5}(2-x)}}{5^{log_{5}(x+4)}}+6x \)
Смотреть решение
