1. Показания счётчика электроэнергии 1 ноября составляли 32947 кВт∙ч, а 1 декабря – 33047 кВт∙ч. Сколько нужно заплатить за электроэнергию за ноябрь, если 1 кВт∙ч электроэнергии стоит 4 руб. 29 коп.? Ответ дайте в рублях.
Смотреть решение
2. На диаграмме показана среднемесячная температура воздуха в январе 1992‐2014 годов. Определите год с наибольшей средней температурой воздуха в январе, в ответе запишите этот год.
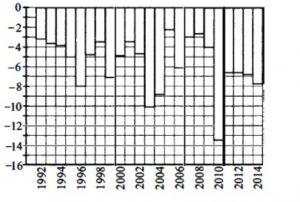
Смотреть решение
3. На клетчатой бумаге с размером клетки 1х1 изображен угол. Найдите синус этого угла
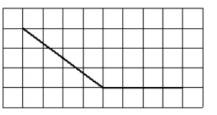
Смотреть решение
4. В школе 51 пятиклассник, среди них – Саша и Настя. Всех пятиклассников случайным образом делят на две группы, по 17 и 34 человек в каждой. Найдите вероятность того, что Саша и Настя окажутся в одной группе. Ответ округлите до сотых.
Смотреть решение
5. Решите уравнение \( \frac{1}{x^2-3x+2}=\frac{1}{2x^2-3x+1} \)Если уравнение имеет более одного корня, в ответе укажите сумму корней.
Смотреть решение
6. На боковой стороне CB равнобедренного (AB=BC) треугольника ABC выбрана точка K. Оказалось, что CA= AK =KB. Найдите угол ABC. Ответ дайте в градусах.
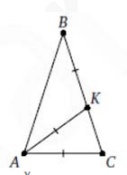
Смотреть решение
7. На рисунке изображен график y=F(x) одной из первообразных некоторой функции , определенной на интервале (-8;3). Определите количество целых чисел xi, для которых f(xi) положительно.
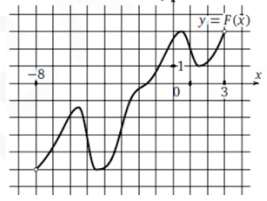
Смотреть решение
8. Образующая конуса наклонена к основанию под углом 60. Найдите площадь основания, если площадь боковой поверхности конуса равна 84.
Смотреть решение
9. Найдите значение выражения :
\( \frac{(a-1)^{1/3}(24-8a)^{1/3}}{(4a-a^2-3)^{1/3}}-\frac{|3a^2-9a-12|}{(a+1)(a-4)} \)
Смотреть решение
10. Небольшой мячик бросают под острым углом к плоской горизонтальной поверхности земли. Максимальная высота полёта мячика, выраженная в метрах, определяется формулой \( H=\frac{v_{0}}{4g}(1-cos2\alpha) \)где v0 = 18 м/c – начальная скорость мячика, а g ‐ ускорение свободного падения (считайте g= 10 м/с2 ). При каком наименьшем значении угла \( \alpha \) (в градусах) мячик может пролететь над стеной высотой 3,5 м на расстоянии не менее 55 cм?
Смотреть решение
11. Виноград содержит 91% влаги, а изюм—7%. Сколько килограммов винограда требуется для получения 21 килограмма изюма?
Смотреть решение
12. Найдите наибольшее значение функции \( y=log_{2}(0.25-x-x^2) \)
Смотреть решение
