1. Про натуральные числа p, q, t известно, что каждое из них больше 8, но меньше 12. Загадали натуральное число, умножили его на р, затем к полученному произведению прибавили q и вычли из результата t. Получили 997. Найдите загаданное число.
Смотреть решение
2. На диаграмме показано распределение выплавки алюминия в 10 странах мира ( в тысячах тонн) за 2009 г. Сколько стран, из представленных на диаграмме, выплавляло алюминия в указанном году больше, чем Германия?
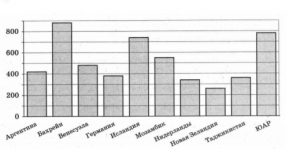
Смотреть решение
3. Найдите площадь четырехугольника, вершины которого имеют координаты (0;2), (4;6), (8;5), (10;0).
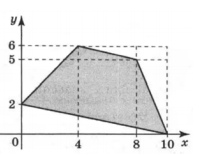
Смотреть решение
4. У Кати в копилке лежит 7 однорублёвых, 6 двухрублевых и 3 пятирублевых монеты. Катя наугад достает из копилки одну монету. Найдите вероятность того, что оставшаяся после этого в копилке сумма составит более 30 рублей.
Смотреть решение
5. Решите уравнение: \( 5*x^{log_{3}2}+2^{log_{3}x}=24 \)
Смотреть решение
6. Окружность, вписанная в равнобедренный треугольник АВС, касается его боковых сторон АВ и АС в точках Т и М соответственно. Найдите ТМ, если АВ = 25, ВС = 14.
Смотреть решение
7. Функция F(x) является первообразной функции \( f(x)=sin^2(x-\frac{\pi}{3})+1 \)Найдите угловой коэффициент касательной к графику функции y=F(x) в точке с абсциссой x0=pi
Смотреть решение
8. Куб вписан в цилиндр, площадь основания которого равна 72\( \pi \) . Найдите площадь поверхности куба.
Смотреть решение
9. Найдите значение выражения
\( ((1-log^2_{2}7)log_{14}2+log_{2}7)5^{log_{5}24} \)
Смотреть решение
10. Мяч бросили вверх так, что пока он не упал на землю, его высота над землей менялась по закону: \( h(t)=1,2+1,9t-t^2 \)где h – высота в метрах, t – время в секундах, прошедшее с момента броска. Сколько процентов от всего времени полета мяча составляет время, в течении которого находится на высоте не более 1,54 метра?
Смотреть решение
11. Моторная лодка плыла сначала 6 минут по озеру, в стоячей воде, а затем 10 минут по реке, против течения. Обратный путь, двигаясь с той же собственной скоростью, лодка прошла за 11 минут. Найдите отношение длины пути, пройденного лодкой по озеру, к длине пути, пройденного ею по реке.
Смотреть решение
12. Найдите наименьшее значение функции:
\( y=e^{4x}-4e^x+8 \)
на отрезке [-2;2]
Смотреть решение
