13. а) Решите уравнение
\( (2\sqrt{3}sin(\pi x+3\pi)-tg(\pi x-\frac{\pi}{2}))*log_{2}(4-x^2)=0 \)
б) Найдите все корни уравнения, принадлежащие отрезку [-1;2]
Смотреть решение
14. В основании пирамиды SABCD лежит ромб АВСD, сторона которого равна 8, а угол
при вершине А равен 600. Известно, что SA=15,SC=√33 и, кроме того, SB = SD.
а) Докажите, что SC – высота пирамиды.
б) Найдите угол между плоскостью ASC и ребром SB.
Смотреть решение
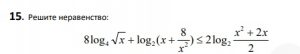
Смотреть решение
16. В треугольнике АВС, площадь которого равна 2, на медианах АК, BL и CN взятысоответственно точки Р, Q и R так, что АР = РК, BQ : QL = 1:2, а CR : RN = 5:4. M – точка пересечения медиан.
а) Докажите, что MR : CN = 1:9.
б) Найдите площадь треугольника PQR.
Смотреть решение
17. Строительной организации необходимо построить некоторое количествоодинаковых домов общей площадью 2500 м2. Стоимость одного дома площадью а м2
складывается из стоимости материалов ( p_{3}a^{1,5} )тысяч рублей, стоимость строительных работ ( p_{2}a ) тысяч рублей и стоимости отделочных работ ( p_{3}a^{0,5} )тысяч рублей. Числа р1,р2, р3 являются последовательными членами геометрической прогрессии, их сумма равна 21, а их произведение равно 64. Если построить 63 дома, то затраты на материалы будут меньше, чем затраты на строительные и отделочные работы. Сколько следует
построить домов, чтобы общие затраты были минимальными?
Смотреть решение
18. Найдите все значения параметра а, при каждом из которых система уравнений
\( x^2+12x+|y|+27=0 \)
\( x^2+(y-a)(y+a)=-12(x+3) \)
Смотреть решение
19. Известно, что квадратное уравнение вида ( x^2+mk+k=0 )имеет два различных
натуральных корня
а) Найдите все возможные значения k при m = -6
б) Найдите все возможные значения m при k-m=45
в) Найдите все возможные значения корней уравнения, если ( k^2-m^2=2236 )
Смотреть решение
