1. Рейс “Москва‐Пекин” вылетел из аэропорта “Домодедово” 1 августа в 18:45 и совершил посадку в аэропорту Пекина 2 августа в 10:00 . Сколько часов занял перелёт, если время вылета и посадки указаны местные, а разность во времени между Пекином и Москвой составляет 5 часов?
Смотреть решение
2. На диаграмме представлено среднее количество солнечных дней в году в различных городах мира. В скольких из этих городов можно выращивать виноград без искусственного досвечивания, если для его вызревания требуется 4 месяца?

Смотреть решение
3. Найдите площадь S (в см2) закрашенного кольца, изображенного на клетчатой бумаге. Сторона клетки равна 1 см. В ответе укажите \( \frac{S}{\pi} \)
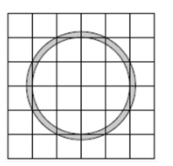
Смотреть решение
4. В зале театра имеется 10 рядов по 20 мест в каждом. Какова вероятность, что в случайно взятом билете номер ряда и номер места окажутся равны?
Смотреть решение
5. Найдите корень уравнения \( (\frac{1}{6})^{log_{2}\frac{1}{x}}=6^{log_{4}(x+2)} \)
Смотреть решение
6. Диагонали параллелограмма ABCD пересекаются в точке O, AB = AO, ∠ ABO = 70°, ∠ ACD = 2∠ CAD. Найдите ∠ ADB. Ответ дайте в градусах.
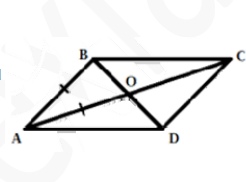
Смотреть решение
7. На рисунке изображён график функции y=f(x) , определенной на интервале (-2;11). Сколько раз график производной этой функции пересекается с осью абсцисс?
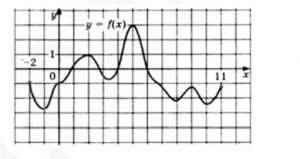
Смотреть решение
8. Из прямоугольного параллелепипеда высотой 1 вырезали куб объёмом 1. Найдите объём исходного параллелепипеда, если площадь основания после вырезания стала равна 7.
Смотреть решение
9. Найдите значение выражения \( \frac{\sqrt{216}*cos(\frac{5 \pi}{4})}{10 sin(\frac{4 \pi}{3})} \)
Смотреть решение
10. Расстояние h, пройденное свободно падающим телом, вычисляется по формуле: \( h=\frac{gt^2}{2} \) где g = 10 м/с2 (ускорение свободного падения), t – время в секундах. На
каком расстоянии от земли (в метрах) будет находиться тело, падающее с высоты 100 м, через 4 с после начала падения?
Смотреть решение
11. Для контроля за перемещениями граждан в районе планируется установить 300 камер, для чего была нанята бригада монтажников. За 10 дней было установлено 20%
камер, после чего один из монтажников заболел, и производительность бригады упала на треть. Бригада продолжила работать, а заболевший, проболев 5 рабочих дней, вышел на работу и присоединился обратно к бригаде, поскольку «горели» сроки, поставленные заказчиком. После его возвращения бригада работала всего на четверть эффективнее, чем пока он болел, а через 3 рабочих дня заболели все рабочие в бригаде. Сколько камер они не успели установить?
Смотреть решение
12. Найдите точку максимума функции \( y=(x^2-28x+28)e^{2-x} \)
Смотреть решение
