1. За год стипендия студента увеличилась на 32%. В первом полугодии стипендия увеличилась на 10%. Определите, на сколько процентов увеличилась стипендия во втором полугодии.
Смотреть решение
2. На рисунке изображены графики, показывающие, как во время телевизионных дебатов между кандидатами А и Б, длившихся ровно 1 час, телезрители голосовали за каждого из них: по горизонтальной оси откладывается время с начала голосования, по вертикальной – число голосов (в тыс.), поданных за это время. Какой процент голосов телезрителей был у кандидата А через 45 минут после начала теледебатов?
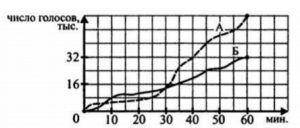
Смотреть решение
3. Найдите площадь пятиугольника АВСDЕ с вершинами в точках А (‐1;0), В (2;5), С (5;3), D(10;6), Е (13;0).
Смотреть решение
4. В шкатулке лежат 6 шаров, 4 из которых – красные. Наугад взяты 3 шара. Какова вероятность того, что все выбранные шары красные?
Смотреть решение
5. Решите уравнение, указав в ответе корень уравнения или сумму корней, если их несколько: \( x\sqrt{5-x}=9\sqrt{5-x} \)
Смотреть решение
6. В треугольнике ABC длины сторон и его площадь связаны соотношением \( S=\frac{\sqrt{3}}{4}(b^2+c^2-a^2) \). Найдите градусную меру угла А.
Смотреть решение
7. Для четной функции f(x) и нечетной функции g(x) для всех действительных значений аргумента выполнено равенство \( f(x)+g(x)=x^2+3x-2 \) Найдите значения выражения \( f'(2)-4g'(3) \)
Смотреть решение
8. Высота правильной треугольной пирамиды в три раза меньше высоты основания пирамиды. Найдите угол между плоскостью боковой грани и плоскостью основания пирамиды. Ответ дайте в градусах.
Смотреть решение
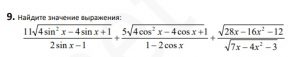
Смотреть решение
10. Вратарь выбросил мяч в поле, направив его под углом 450 к поверхности поля. Пока мяч не упал, высота, на которой он находится, описывается формулой \( h(t)=-5t^2+12t+1.25 \) ( h – высота в метрах, t – время в секундах, прошедшее с момента удара). Пренебрегая сопротивлением воздуха, считаем, что горизонтальная составляющая скорости мяча не меняется в полете. Определите, на каком расстоянии от вратаря в метрах мяч приземлится на поле.
Смотреть решение
11. Гекльберри Финн может покрасить весь забор за 3 часа, а Том Сойер покрасил бы за это время треть забора. Друзья начали работу вместе, но через некоторое время Том Сойер убежал к Бекки. В результате Гекльберри Финн закончил работу один, и весь забор был покрашен за 2 часа 54 минуты. Найдите количество минут, затраченных на работу Томом Сойером.
Смотреть решение
12. Найдите наибольшее значение функции: \( y=4(12sin^2x+15cosx-4cos^3x) \)
Смотреть решение
