1. В копилке находятся монеты достоинством 2 рубля и 5 рублей. Известно, что без монет копилка весит 100 г, а с монетами 270 г. Монет достоинством 5 рублей в копилке 10 шт. Сколько денег (в руб.) находится в копилке, если монеты достоинством 2 рубля и 5 рублей соответственно весят 3 г и 6,5 г?
Смотреть решение
2. На диаграмме показана среднемесячная температура воздуха (в градусах Цельсия) в Челябинске. Найдите количество месяцев со среднемесячной температурой выше 100С.
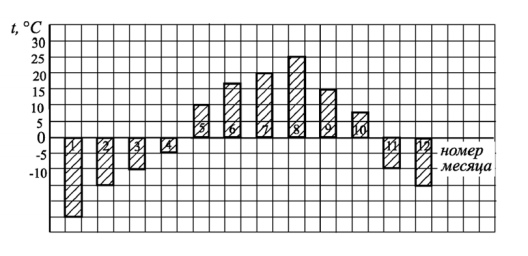
Смотреть решение
3. Найдите площадь закрашенной фигуры на координатной плоскости (см. рис.).
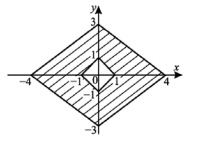
Смотреть решение
4. Известно, что в среднем 95% выпускаемой продукции удовлетворяет стандарту. Упрощенная схема контроля признает пригодной продукцию с вероятностью 0,98, если она стандартна, и с вероятностью 0,06, если она нестандартна. Определить вероятность того, что взятое наудачу изделие пройдет упрощенный контроль?
Смотреть решение
5. Решите уравнение: \( (9^{2x+5}*(\sqrt{3})^{2x})^x=(\frac{1}{3})^{-x-2} \) Если корней несколько, в ответе укажите наименьший из них.
Смотреть решение
6. В равнобедренном треугольнике MNK (NK = MK) проведены высоты MP и NF. Известно, что PF = 3, а косинус угла К равен 0,3. Найдите длину стороны MN.
Смотреть решение
7. Прямая, заданная уравнением \( y=bx+1 \) при некотором значении b является касательной к графику функции \( f(x)=\frac{1}{1+x} \). Найдите b.
Смотреть решение
8. Шар пересечён двумя параллельными плоскостями, расположенными по одну сторону от его центра. Радиус первого сечения равен 12, радиус второго сечения равен 9. Расстояние от центра шара до плоскости первого сечения равно 9. Найдите расстояние между плоскостями сечений.
Смотреть решение
9. Найдите значение выражения \( tg(2acrctg(-\frac{\sqrt{3}}{3})-\frac{\pi}{3}) \)
Смотреть решение
10. Расстояние (в км) от наблюдателя, находящегося на высоте h (в м) от поверхности Земли, до наблюдаемой им линии горизонта вычисляется по формуле: \( l=\sqrt{\frac{R*h}{500}} \) где R = 6400 км – радиус Земли. Наблюдатель, находящийся на небольшой высоте, видит горизонт на расстоянии 13,6 км. На сколько метров еще надо подняться, чтобы горизонт был виден на расстоянии 16 км?
Смотреть решение
11. Бетономешалка содержит раствор цемента, состоящий из цемента, песка и воды. Из бетономешалки вылили \( \frac{2}{5} \) находящегося в ней раствора цемента, а к оставшейся
части добавили некоторое количество песка и некоторое количество воды так, что бетономешалка оказалась заполненной на \( \frac{7}{9} \) первоначального объема раствора. При этом раствор цемента стал содержать 27% цемента. Сколько процентов цемента изначально было в растворе?
Смотреть решение
12. Найдите наибольшее значение функции \( f(x)=log_{7}(\frac{1}{x^3-12x^2+45x-1}) \) на [3;6]
Смотреть решение
