1. Установка двух счётчиков воды (холодной и горячей) стоит 3300 рублей. До установки счётчиков за воду платили 800 рублей ежемесячно. После установки счётчиков ежемесячная оплата воды стала составлять 300 рублей. Через какое наименьшее количество месяцев экономия по оплате воды превысит затраты на установку счётчиков, если тарифы на воду не изменятся?
Смотреть решение
2. Междугородний автобус курсирует между Москвой и Сергиевым Посадом с остановкой в Пушкино. Путь в один конец занимает 1,5 часа, остановка в Пушкино длится 10 минут, и в каждом конечном пункте у автобуса стоянка в течение получаса. На рисунке ниже показан график движения автобуса, выезжающего из Москвы в 7:00 утра, когда автобус следует точно по расписанию. По пути из Москвы в Пушкино автобус задержался и выехал из Пушкино в Сергиев Посад на 10 минут позже. На сколько км/ч необходимо увеличить скорость автобуса, чтобы в Сергиев Посад он прибыл точно по расписанию?
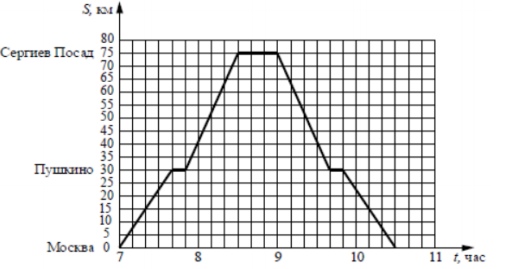
Смотреть решение
3. На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.

Смотреть решение
4. На фабрике керамической посуды 20% произведенных тарелок имеют дефект. При контроле качества продукции выявляется 70% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
Смотреть решение
5. Решите уравнение \( \frac{\sqrt{x^2+x+1}}{x+1}=\frac{x^2+x+1}{x+1} \)Если уравнение имеет более одного корня, то в ответе запишите сумму всех корней.
Смотреть решение
6. В прямоугольном треугольнике АВС угол С – прямой. СН – высота. АН=5, ВН=4. Найдите катет СВ.
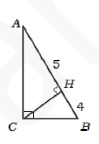
Смотреть решение
7. На рисунке изображен график \( y=f'(x) \) производной функции \( f(x) \), определенной на интервале (-6;7) . В какой точке отрезка [-4;2] функция \( f(x) \) принимает наименьшее
значение?
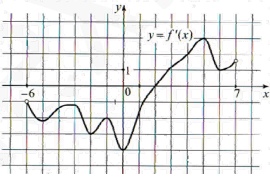
Смотреть решение
8. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60. Высота пирамиды равна 6. Найдите объем пирамиды.
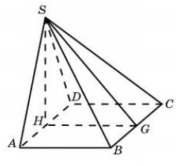
Смотреть решение
9. Найдите значение выражения \( \frac{4}{\sqrt{2+\sqrt{3}}sin15} \)
Смотреть решение
10. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 40 см.Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 до 60 см, а расстояние d2 от линзы до экрана – в пределах от 180 до 200 см. Изображение на экране будет четким, если выполнено соотношение \( \frac{1}{d1}+\frac{1}{d2}=\frac{1}{f} \)Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображениена экране было чётким. Ответ выразите в сантиметрах.
Смотреть решение
11. Из молока, жирность которого 5%, делают творог жирностью 15,5%, при этом остается сыворотка жирностью 0,5%. Сколько килограммов творога получится из одной тонны молока?
Смотреть решение
12. Найдите наименьшее значение функции \( y=e^{2x}-6e^x+3 \) на отрезке [1;2]
Смотреть решение
