1. Производительность труда выросла на 14%, поэтому работа была выполнена на 21 день быстрее плана. За сколько дней была выполнена работа?
Смотреть решение
2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали – значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 8‐го августа. Ответ дайте в градусах Цельсия.
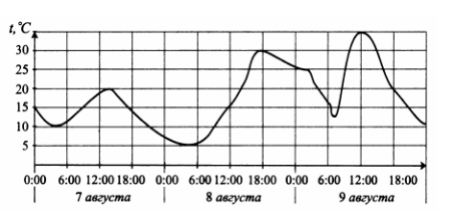
Смотреть решение
3. Найдите площадь S трапеции ABCD, изображенной на рисунке. В ответе укажите \( \frac{S}{\sqrt{3}} \)
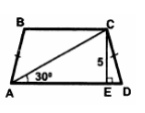
Смотреть решение
4. В зале театра имеется 10 рядов по 20 мест в каждом. Какова вероятность, что в случайно взятом билете номер ряда и номер места окажутся равны?
Смотреть решение
5. Решите уравнение \( \frac{5}{log_{2}x+3}+\frac{4}{log_{2}x}=3 \) Если корней несколько, в ответе укажите их произведение.
Смотреть решение
6. Найдите градусную меру угла САВ, изображенного на рисунке, при условии, что угол АСВ тупой.
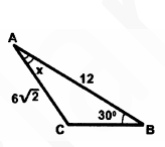
Смотреть решение
7. На рисунке изображен график четной функции \( y=g(x) \) на отрезке[-4;0] Функция определена на всей числовой оси. Вычислите \( g(4)+2g(1)-\frac{g(0)}{g(2)} \)
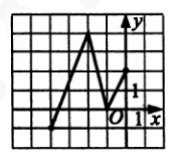
Смотреть решение
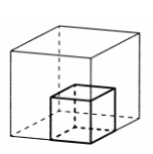
8. Масса однородного бетонного куба равна 0,5 т. Сколько тонн будет составлять масса куба, сделанного из того же бетона, но ребро которого в 2 раза больше, чем ребро маленького кубика?
Смотреть решение
9. Найдите значение выражения \( 3^{log_{9}(x+2\sqrt{x-2}-1)}+7^{log_{49}(x-2\sqrt{x-2}-1)} \) при \( x=2,01 \)
Смотреть решение
10. Груз массой 0,4 кг колеблется на пружине. Его скорость v меняется по закону \( v=v_{0}cos\frac{2\pi t}{T} \) где t — время с момента начала колебаний,T=2 с— период
колебаний, v0 = 6,0 м/с. Кинетическая энергия E (в джоулях) груза вычисляется по формуле \( E=\frac{mv^2}{2} \) где — масса груза в килограммах, — скорость груза в м/с. Найдите кинетическую энергию груза через 36 секунд после начала колебаний. Ответ дайте в джоулях.
Смотреть решение
11. Сумма вклада за третий год увеличилась на 54 рубля, а за шестой год – на 128 рублей. Какова была величина вклада в рублях в начале четвертого года, если доход начисляется в конце каждого года хранения вклада и процентная ставка не менялась?
Смотреть решение
12. Найдите точки экстремума функции. Если их несколько, в ответ запишите ихсумму \( f(x)=\frac{6x-x^3}{x+1}*3^{log_{3}(x+1)}+\frac{(x^3+2)(\sqrt{3-x})^2}{x-3} \)
Смотреть решение
