1. Затраты на покупку огурцов возросли на 92%, а цена килограмма огурцов увеличилась на 60%. На сколько процентов увеличился вес купленных огурцов?
Смотреть решение
2. На тренировке в 50‐метровом бассейне пловец проплыл 200‐метровую дистанцию. На рисунке изображен график зависимости расстояния (в метрах) между пловцом и точкой старта от времени движения t (в секундах) пловца. Определите по графику, какое расстояние преодолел пловец за 2 мин 20 с.
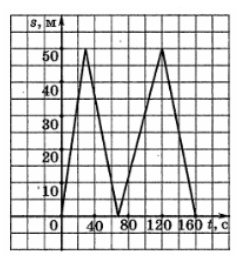
Смотреть решение
3. Найдите косинус угла АВС, изображенного на рисунке
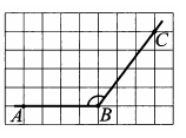
Смотреть решение
4. Из шести букв разрезной азбуки составлено слово «АНАНАС». Ребенок, не умеющий читать, рассыпал эти буквы, а затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово «АНАНАС». Ответ округлите до тысячных.
Смотреть решение
5. Найдите x0‐ наибольший отрицательный корень уравнения В ответе укажите \( \frac{x_{0}}{\pi} \)
\( \sqrt{-3sinx+cosx}=\sqrt{sinx-3cosx} \)
Смотреть решение
6. Две окружности с центрами в точках О и О1 и радиусами 5 и 3 соответственно касаются сторон угла А (В и В1 – точки касания). Найдите расстояние между центрами окружностей, если АВ1=4. Ответ округлите до десятых.
Смотреть решение
7. Точка движется по координатной прямой согласно закону \( x(t)=3+2t+t^2 \), где x(t)-координата точки в момент времени t . В какой момент времени скорость
точки будет равна 5?
Смотреть решение
8. Четырехугольная пирамида весом 27 кг горизонтальными плоскостями разрезана на 3 части одинаковой высоты. Найдите вес в килограммах нижней части пирамиды.
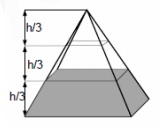
Смотреть решение

Смотреть решение
10. Водолазный колокол, содержащий \( v=3 \) моль воздуха при давлении p1=1,8 атмосферы, медленно опускают на дно водоема. При этом происходит сжатие воздуха до конечного давления p2.Работа, совершаемая водой при сжатии воздуха, определяется выражением\( A=avTlog_{2}\frac{p2}{p1} \), где \( a=7,9 \) Дж/моль*К, постоянная, T=300 К ‐ температура воздуха. Найдите, какое давление p2 (в атмосферах) будет иметь воздух в колоколе, если при сжатии воздуха будет совершена работа в 14 220 Дж.
Смотреть решение
11. Поезд отправился со станции А, проследовал через станции В и С, прибыл на станцию D. Пусть ВС больше АВ на \( \frac{1}{4} \) часть АВ, а CD на 60% меньше ВС. Найдите
среднюю скорость поезда на пути AD, если его скорость на АВ, ВС и CD равнялась соответственно 80 км/ч, 100 км/ч, 180 км/ч. Ответ дайте в км/ч.
Смотреть решение
12. Найдите точку минимума функции \( y=ln(2x+5)+\frac{2}{(2x+5)^2} \)
Смотреть решение
