1. Яблоки подешевели на 20%. Сколько килограмм яблок можно теперь купить на те же деньги, на которые раньше покупали 2,8 кг яблок?
Смотреть решение
2. На графике показано изменение температуры воздуха на протяжении трех суток, начиная с 0 часов 2 марта. На оси абсцисс отмечается время суток в часах, на оси ординат – значение температуры в градусах. Найдите по графику наибольшую температуру воздуха 3 марта в градусах Цельсия.
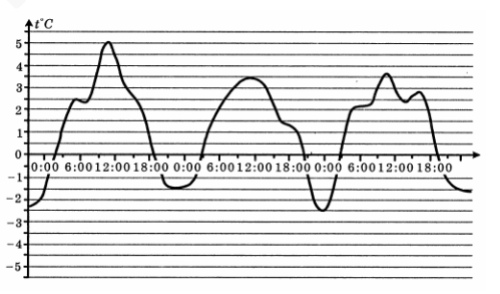
Смотреть решение
3. Внутри параллелограмма ABCD, площадь которого равна 10, отмечена точка М. Найдите сумму площадей треугольников AMВ и CMD.
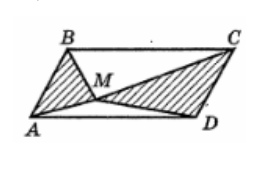
Смотреть решение
4. Бросаются одновременно две игральные кости. Найдите вероятность того, что сумма выпавших очков будет больше, чем их произведение. Ответ округлите до сотых.
Смотреть решение
5. Решите уравнение \( \sqrt{15x^2+2x+8}+4x=0 \) Если уравнение имеет более одного корня, в ответе укажите больший из корней.
Смотреть решение
6. В равнобедренном треугольнике АВС с основанием АС высоты ВМ и АН пересекаются в точке К, причем АК=5, КН=3. Найдите площадь треугольника АВК.
Смотреть решение
7. На рисунке изображен график производной функции y=f(x), заданной на отрезке [-2;6] Найдите число точек на этом отрезке, в которых касательная к графику функции f(x)параллельна биссектрисе первой четверти.
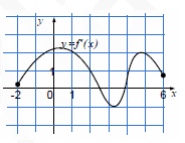
Смотреть решение
8. Боковое ребро правильной треугольной призмы на 20% больше ее стороны основания. Расстояние между серединами двух непараллельных ребер, принадлежащих разным основаниям, равно 13. Найдите площадь боковой поверхности призмы.
Смотреть решение
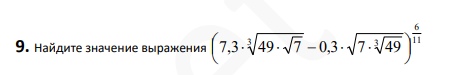
Смотреть решение
10. В ходе распада радиоактивного изотопа его масса уменьшается по закону
\( m(t)=m_{0}2^{-\frac{t}{T}} \) где m0 – начальная масса изотопа, t (мин) – прошедшее от начального момента время, T ‐ период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени m0=156 мг изотопа, период полураспада которого T=8 мин В течение скольких минут масса изотопа будет не меньше 39 мг?
Смотреть решение
11. Двум операторам поручили набрать на компьютере текст книги объемом 315 страниц. Один оператор, отдав второму 144 страницы книги, взял остальные страницы себе. Первый выполнил свою работу за 19 дней, а второй свою – за 12. На сколько процентов нужно было увеличить часть работы второго оператора (уменьшив часть работы первого), чтобы они, работая с прежней производительностью, выполнили свою работу за одинаковое число дней?
Смотреть решение
12. Найдите наибольшее значение функции \( y=3x-e^{3x} \) на отрезке [-1;1]
Смотреть решение
