1. Виктор въехал на участок дороги протяженностью 2,1 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на этом
участке 60 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Виктор въехал на участок в 10:08:07, а покинул его в 10:09:52. На сколько км/ч его скорость отличалась от максимально разрешенной?
Смотреть решение
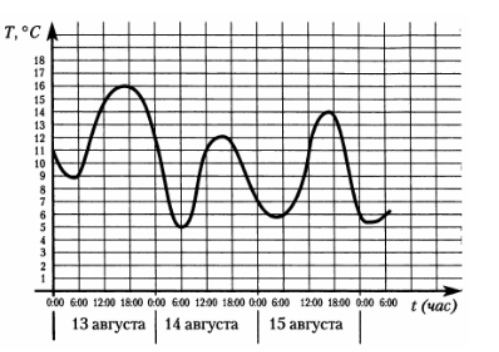
2. На графике показано изменение температуры воздуха на протяжении трех суток. На оси абсцисс отмечается время суток в часах. На оси ординат – значение
температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 15 августа. Ответ дайте в градусах Цельсия.
Смотреть решение
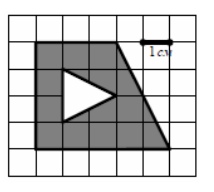
3. Найдите площадь заштрихованной части фигуры, изображенной на клетчатой бумаге с размером клетки 1 см × 1 см (см. рисунок). Ответ дайте в квадратных
сантиметрах.
Смотреть решение
4. В урне находится 6 шаров: 1 белый, 2 красных и 3 черных. Наугад вытаскивают 3 шара. Какова вероятность того, что среди вытащенных шаров ровно 1 будет черным?
Смотреть решение
5. Найдите произведение всех корней уравнения \( (10+3x-x^2)^{1/3}*lg(7-x-x^2)=0 \)
Смотреть решение
6. В треугольнике АВС угол С равен 76°, AL и BM – биссектрисы углов А и В, пересекающиеся в точке О. Найдите угол АОВ (в градусах).
Смотреть решение
7. Функция \( y=f(x) \)определена на промежутке (‐2;7). На рисунке изображен график ее производной. Найдите абсциссу точки, в которой функция принимает наибольшее значение.
Смотреть решение
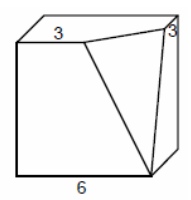
8. Найдите объем части куба, изображенной на рисунке.
Смотреть решение
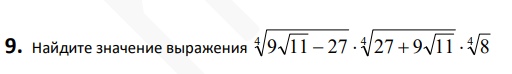
Смотреть решение
10. Рейтинг R интернет‐магазина вычисляется по формуле
\( R=r_{пок}-\frac{r_{пок}-r_{экс}}{(k+1)^{\frac{0,03K}{r_{пок}+0,59}}} \)
где \( r_{пок} \) ‐ средняя оценка магазина покупателями (от 0 до 1), \( r_{экс} \)‐ оценка магазина экспертами (от 0 до 0,7) К ‐ число покупателей, оценивших магазин. Найдите рейтинг интернет‐магазина, если число покупателей, оставивших отзыв о магазине, равно 24, их средняя оценка равна 0,85, а оценка экспертов равна 0,1.
Смотреть решение
11. Два пешехода вышли одновременно из пунктов А и В навстречу друг другу. Они встретились в 50 м от пункта В, а затем, дойдя до А и В, пошли обратно и вновь
встретились в 25 м от А. Найдите расстояние АВ в метрах, если известно, что они двигались равномерно и непрерывно.
Смотреть решение
12. Найдите точку минимума функции \( y=(x-0,5)*sinx+cosx \) на промежутке (0;pi/2)
Смотреть решение
