1. Для распечатки 302 страниц были использованы две копировальные машины. Первая работала 8 минут, вторая 10 минут. Сколько страниц в минуту печатает первая
машина, если первая печатает в минуту на 4 страницы больше, чем вторая?
Смотреть решение
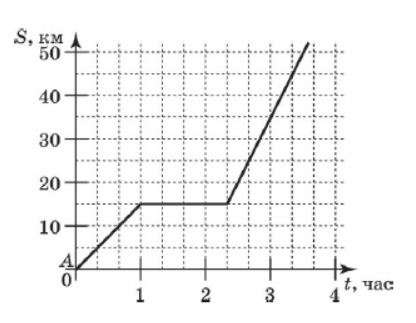
2. На рисунке изображен график, описывающий прямолинейное движение автомобиля. По горизонтальной оси отложено время (в часах), по вертикальной —
расстояние от пункта А (в километрах). Известно, что через 180 минут после начала движения автомобиль достиг пункта В и продолжил движение. Определите расстояние в километрах между пунктами А и В.
Смотреть решение
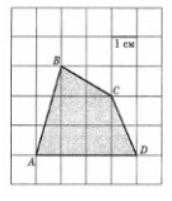
3. Найдите площадь четырехугольника ABCD. Размер каждой клетки 1см х 1 см. Ответ выразите в квадратных см.
Смотреть решение
4. Петя и Таня независимо друг от друга загадывают по одной цифре. С какой вероятностью сумма этих цифр окажется больше 16?
Смотреть решение
5. Найдите корень уравнения \( (0,2)^{x+3}=\frac{1}{5}(0,04)^{x} \)
Смотреть решение
6. Найдите периметр параллелограмма ABCD, если AD=10, BD=8, а отрезок, соединяющий вершину В с серединой стороны AD, равен √15
Смотреть решение
7. Наблюдение за космическим телом показало, что расстояние S (в километрах) между этим телом и Землей увеличивается по закону \( S=1,8*10^5+0,5*10^5\sqrt{t} \) где
t — время в секундах от момента начала наблюдения. Через сколько секунд после начала наблюдения скорость удаления тела от Земли составит \( 10^3 \) км/с?
Смотреть решение
8. Точки M и N расположены на окружностях верхнего и нижнего основания цилиндра, радиус основания которого равен 2, а высота — 3. Длина отрезка MN равна 4. Через отрезок MN проведена плоскость, параллельная образующей цилиндра. Найдите расстояние от оси цилиндра до этой плоскости.
Смотреть решение
9. Найдите значение выражения \( (2+\sqrt{5})^{\frac{1}{3}}+(2-\sqrt{5})^{\frac{1}{3}} \)
Смотреть решение
10. Плоский замкнутый контур площадью \( S=0,5 \) м^2, находится в магнитном поле, индукция которого равномерно возрастает. При этом согласно закону электромагнитной
индукции Фарадея в контуре появляется ЭДС индукции, значение которой, выраженное в вольтах, определяется формулой \( E=aScosα \), где α – острый угол между направлением магнитного поля и перпендикуляром к контуру, \( a=4*10^{-4} \) Тл/спостоянная, S – площадь замкнутого контура, находящегося в магнитном поле (в м2).
При каком минимальном угле α (в градусах) ЭДС индукции не будет превышать \( 10^{-4} \) В?
Смотреть решение
11. Первый раствор содержит 20% азотной кислоты и 80% воды, второй ‐ 60% кислоты и 40% воды. Первая смесь была получена из 15 л первого раствора и некоторого количества второго раствора. Смешав то же самое количество второго раствора с 5 л первого раствора, получили вторую смесь. Сколько литров второго раствора было использовано для приготовления первой смеси, если процентное содержание воды во второй смеси вдвое больше процентного содержания кислоты в первой?
Смотреть решение
12. Найти наименьшее значение функции
\( f(x)=|\sqrt{-x^2+6x-5}-3|+\sqrt{-x^2+6x-5}+x^3+6x^2 \)
Смотреть решение
