1. На кладку камина уходит 320 кирпичей, и еще 20% от этого количества кирпичей уходит на кладку трубы. Какое максимальное число каминов с трубой можно сложить
из 10 000 кирпичей?
Смотреть решение
2. На диаграмме показан график скорости потребления воды Краснодарской ТЭЦ в течение суток. Какой наибольший объем воды (в куб. м) потребит станция за 6 часов непрерывной работы?
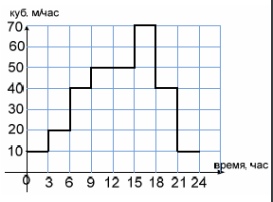
Смотреть решение
3. Найдите площадь заштрихованной фигуры
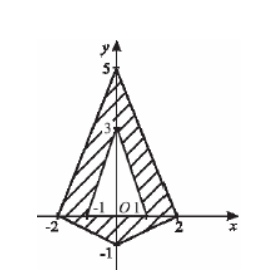
Смотреть решение
4. Даны три цифры {0;1;3}. Найдите вероятность того, что эти цифры, расположенные в случайном порядке, составят нечетное число, большее числа 10. (Число не может
начинаться с нуля)
Смотреть решение
5. Решите уравнение \( log_{3}(x^2-6)=log_{3}(x-2)+1 \) Если корней несколько, в ответе укажите меньший корень.
Смотреть решение
6. Центр О окружности радиуса 6 принадлежит биссектрисе угла 60. Найдите радиус окружности, вписанной в данный угол и касающейся данной
окружности, как показано на рисунке.

Смотреть решение
7. На рисунке изображен график некоторой функции y=f(x),Пользуясь графиком, вычислите интеграл \( \int\limits_{-2}^4f(x)dx \)
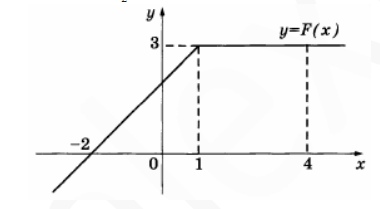
Смотреть решение
8. Высота основания правильной треугольной пирамиды равна 9, а высота боковой грани пирамиды, проведенная к ребру основания, равна √73. Найдите боковое
ребро пирамиды.
Смотреть решение
9. Найдите значение выражения \( m^2+n^2 \), если для натуральных чисел m и n
\( (m+n)^{1/2}=\sqrt{13}(m-n)^{-1/2} \)
Смотреть решение
10. Масса радиоактивного вещества уменьшается по закону \( m(t)=m_{0}2^{-\frac{1}{T}} \)где m0 – начальная масса, а T-период полураспада. В лаборатории получили вещество,
содержащее m0=12 мг изотопа меди‐64, период полураспада которого T=12,8 часов. Через сколько часов количество меди‐64 уменьшится до 3 мг.
Смотреть решение
11. В гору ехал автомобиль. В первую секунду после достижения пункта A он проехал 30 м, а в каждую следующую секунду он проезжал на 2 м меньше, чем в предыдущую.
Через 9 с после того, как автомобиль достиг пункта A, навстречу ему выехал автобус из пункта B, находящегося на расстоянии 258 м от пункта A. В первую секунду автобус проехал 2 м, а в каждую следующую секунду он проезжал на 1 м больше, чем в предыдущую. Какое расстояние в метрах проехал автобус до встречи с автомобилем?
Смотреть решение
12. Найдите наибольшее значение функции \( y=x^3+8x^2+16x+23 \) на отрезке [-13;-3]
Смотреть решение
