1. Три числа относятся как 5:6:10. Если первое число уменьшить на 10%, а второе — на 20%, то на сколько процентов надо увеличить третье число, чтобы их сумма не изменилась?
Смотреть решение
2. На рисунке изображен график, описывающий прямолинейное движение автобуса. По горизонтальной оси отложено время (в часах), по вертикальной — расстояние от
пункта А (в километрах). Выехав из пункта A в пункт B, автобус через некоторое время должен был снизить скорость из‐за ремонта шоссе. Используя график движения автобуса, определите длину ремонтируемого участка шоссе (в километрах).

Смотреть решение
3. В параллелограмме ABCD известны координаты трех вершин: A(–1; 3), B(2; 4), C(7; 8). Найдите ординату точки D.
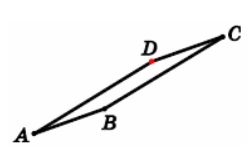
Смотреть решение
4. В первой коробке 20 ламп, из них 18 стандартных. Во второй коробке – 10 ламп, из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую.
Найдите вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной.
Смотреть решение
5. Решите уравнение \( log_{30-3*2^x}(2^x-3)^2=log_{2^x-2}(2^x-3)^2 \) Если корней несколько, в ответе укажите их сумму.
Смотреть решение
6. Найдите длину общей касательной двух окружностей, радиусы которых равны 4 и 1, касающихся внешним образом

Смотреть решение
7. На рисунке изображен график некоторой функции y=f(x) Одна из первообразных этой функции равна \( F(x)=-\frac{1}{3}x^3-2,5x^2-4x+2 \)Найдите площадь заштрихованной фигуры.
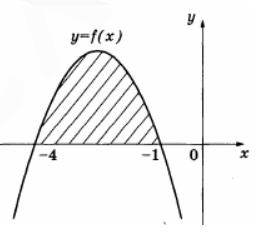
Смотреть решение
8. Площадь боковой поверхности конуса равна 16 см2. Радиус основания конуса уменьшили в 4 раза, а образующую увеличили в 2 раза. Найдите площадь боковой поверхности получившегося конуса. Ответ дайте в см2.
Смотреть решение
9. Найдите значение выражения \( log_{\sqrt{ab}}(\frac{a^{\frac{1}{5}}}{b^{\frac{1}{8}}}) \), если \( log_{ab}a=5 \)
Смотреть решение
10. Деталью некоторого прибора является вращающаяся катушка. Она состоит из трeх однородных соосных цилиндров: центрального массой m=6 кг и радиуса R=`5 см, и двух боковых с массами M=1 кг и с радиусами R+h При этом момент инерции катушки относительно оси вращения, выражаемый в кг ∙ см2 , задаeтся формулой
\( I=\frac{(m+2M)R^2}{2}+M(2Rh+h^2) \)
При каком максимальном значении h момент инерции катушки не превышает
предельного значения 1300 кг ∙ см2? Ответ выразите в сантиметрах
Смотреть решение
11. В баке находится 100 литров смеси кислоты с водой. Из бака отлили часть смеси и добавили равное по объёму количество воды, которое на 10 литров превышает первоначальное количество кислоты в смеси. Затем снова отлили такое же количество смеси, как в первый раз, в результате чего количество кислоты в баке уменьшилось в четыре раза по сравнению с количеством её в исходной смеси. Определить количество воды в исходной смеси в литрах.
Смотреть решение
12. Найдите минимум функции \( y=5\frac{3}{4}+3x+\frac{x^2}{2}-x^3-\frac{x^4}{4} \)
Смотреть решение
