1. Некоторая сумма, большая 1000 рублей, была помещена в банк, и после первого года хранения проценты, начисленные на вклад, составили 400 рублей. Владелец вклада добавил на счет еще 600 рублей. После второго года хранения и начисления процентов сумма на вкладе стала равной 5500 рублям. Какова была первоначальная сумма вклада в рублях, если процентная ставка банка для первого и второго годов хранения была одинакова?
Смотреть решение
2. На диаграмме показано число ручек, карандашей, линеек и ластиков, проданных магазином за одну неделю. Названия предметов отсутствуют на данной диаграмме. Ручки продавались наиболее часто. Ластиков было продано меньше, чем любых других предметов. Карандашей было продано больше, чем линеек. Сколько линеек было продано?
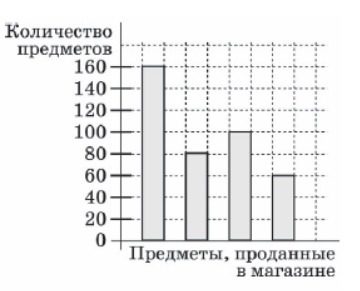
Смотреть решение
3. Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.
Смотреть решение
4. На плоскости нарисованы две концентрические окружности, радиусы которых 3 см и 5 см. Какова вероятность того, что точка, брошенная наудачу в больший круг, попадет в кольцо, образованное этими окружностями?
Смотреть решение
5. Решите уравнение \( 1+log_{9}(x+1)^2=log_{3}(3x+9) \)
Смотреть решение
6. В трапеции ABCD с основаниями ВС и AD из точки М, середины стороны CD, проведен к стороне АВ перпендикуляр ВМ длиной 6 см. Найдите периметр трапеции, если АВ=9 см и CD=8 см.
Смотреть решение
7. На рисунке изображен график первообразной y=F(x) некоторой функции y=f(x) определенной на интервале (-16;-2) Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-10;-4]
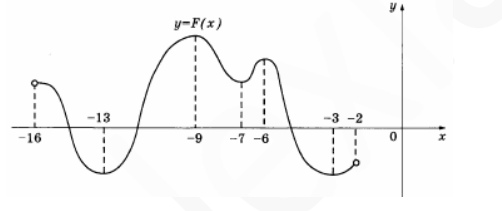
Смотреть решение
8. Через точку окружности основания цилиндра проведены два сечения: одно через ось цилиндра, а второе параллельно ей. Угол между плоскостями сечений равен 45°. Площадь боковой поверхности цилиндра равна 18pi√2. Найдите меньшую из площадей данных сечений.
Смотреть решение
9. Найдите значение выражения \( \frac{2\sqrt{7}+\sqrt{63}-\sqrt{175}}{\sqrt{5}-\sqrt{3}} \)
Смотреть решение
10. Для поддержания навеса планируется использовать цилиндрическую колонну. Давление (в паскалях), оказываемое навесом и колонной на опору, определяется по
формуле \( P=\frac{4mg}{\pi D^2} \)где m – их общая масса, D(в метрах) – диаметр колонны. Считая ускорени падения g равным 10 м/с2 , а pi равным 3, определите наименьший возможный диаметр колонны (в метрах), если давление, оказываемое на опору, не должно быть больше 400 000 Па.
Смотреть решение
11. Два поезда выехали одновременно в одном направлении из городов A и B, расположенных на расстоянии 60 км друг от друга, и одновременно прибыли на станцию C. Если бы один из них увеличил свою скорость на 25 км/ч, а другой – на 20 км/ч, то они прибыли бы одновременно на станцию C, но на 2 часа раньше. Найдите скорости поездов в км/ч, в ответе укажите их сумму.
Смотреть решение
12. Найдите наименьшее значение функции \( f(x)=(2-cos^2x-cos^4x)(1+ctg^2x) \)
Смотреть решение
