1. Юрий Деточкин хочет отправить маме перевод на 10 тыс. рублей. Банкомат за осуществление этой операции взимает комиссию: 80 руб. + 10% от суммы перевода. Какую сумму в рублях должен внести Юрий в банкомат, чтобы его мама получила ровно 10 тыс. рублей?
Смотреть решение
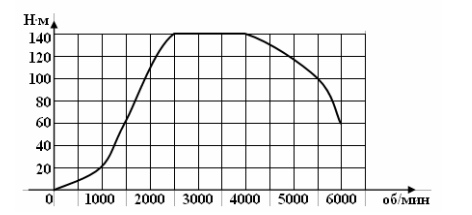
2. На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси
ординат – крутящий момент в Н∙м. Скорость автомобиля (в км/ч) приближенно выражается формулой v = 0,036n, где n – число оборотов двигателя в минуту. С какой наибольшей скоростью может двигаться автомобиль, чтобы крутящий момент был равен 140 Н∙м? Ответ дайте в километрах в час.
Смотреть решение
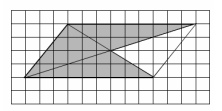
3. Клетка имеет размер 1 см * 1 см. Найдите площадь закрашенной фигуры. Ответ дайте в квадратных сантиметрах.
Смотреть решение
4. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,5 погода завтра будет такой же, как и сегодня. Сегодня 23 февраля, погода в Волшебной стране хорошая. Найдите вероятность того, что 8 марта в Волшебной стране будет отличная погода (Считать, что 2020‐м году в феврале 29 дней)
Смотреть решение
5. Найдите корень уравнения \( (2x-1,4)^3=-512 \)
Смотреть решение
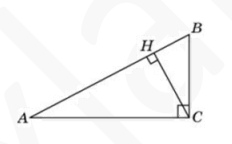
6. В треугольнике ABC угол C равен 90°, CH – высота, угол В равен 60°, AB = 10. Найдите АH.
Смотреть решение
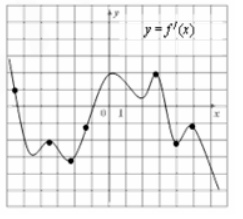
7. На рисунке изображён график y =f'(x) производной функции f (x). На графике отмечены семь точек. Сколько из этих точек принадлежит промежуткам убывания функции f(x).
Смотреть решение
8. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, если известно, что высота призмы равна 6.
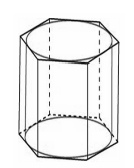
Смотреть решение
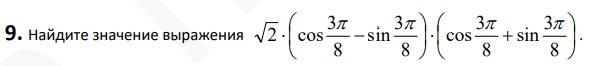
Смотреть решение
10. Высота над землёй подброшенного вверх мяча меняется по закону h(t)=0,2+14-5t^2, где h – высота в метрах, t – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте более 10 метров?
Смотреть решение
11. Имеется два сплава. Первый сплав содержит 5% меди, второй – 95% меди. Масса второго сплава меньше массы первого на 90 кг. Из этих двух сплавов получили третий сплав, содержащий 45% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Смотреть решение
12. Найдите точку максимума функции \( (6-4x)*cosx+4sinx+4 \), принадлежащую промежутку (-0,5pi;pi)
Смотреть решение
