1. Некоторое число уменьшили на 20%. На сколько процентов надо увеличить результат, чтобы получить первоначальное число?
Смотреть решение
2. На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8‐го класса по обществознанию в 2007 году (по 1000‐бальной шкале). По данным диаграммы найдите число стран, в которых средний балл участников не меньше, чем 515.
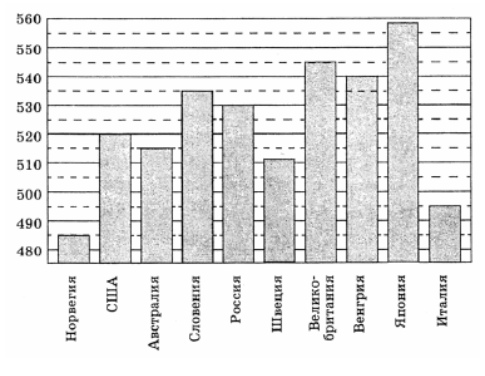
Смотреть решение
3. Центральный угол на 360 больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
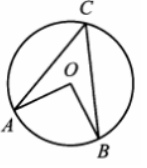
Смотреть решение
4. Пенсионер гуляет по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Пенсионер начинает прогулку в точке А. Найдите вероятность того, что он придет в точку G.
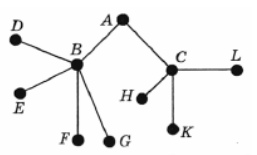
Смотреть решение
5. Решить уравнение \( log_{1/8}x+5log_{4}x+log_{\sqrt{2}}x=16\frac{2}{3} \)
Смотреть решение
6. Найдите площадь равнобедренной трапеции, если ее диагональ, равная 10, образует с основанием угол, косинус которого равен \( \frac{\sqrt{2}}{10} \)
Смотреть решение
7. На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке xo Уравнение касательной дано на рисунке. Найдите
значение производной функции y=2f(x)-1 в точке xo.
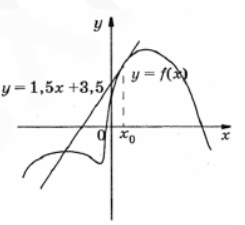
Смотреть решение
8. В правильной треугольной пирамиде SABC ребра ВА и ВС разделены точками K и L так, что ВК=BL=4 и KA=LC=2. Найдите угол между плоскостью основания АВС и плоскостью сечения SKL. Ответ выразите в градусах.
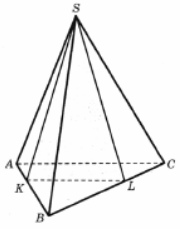
Смотреть решение

Смотреть решение
10. Автомобиль разгоняется с места с постоянным ускорением a=0,2 м/с^2 и через некоторое время достигает скорости v=7 м/с. Какое расстояние к этому моменту
прошел автомобиль? Ответ выразите в метрах. Скорость v, пройденный путь l , время разгона t и ускорение a связаны соотношениями v=at, l=at^2/2.
Смотреть решение
11. Из города в деревню одновременно отправились бегун Б и пешеход П1 , а в тот же момент из деревни в город вышел пешеход П2 . Скорости пешеходов были равны.
Встретившись, Б и П2 некоторое время стояли на месте, а затем направились в деревню. При этом Б побежал с прежней скоростью, равной 12 км/ч, а П2 уменьшил свою скорость в полтора раза. В результате в деревню сначала прибежал Б, а затем через промежуток времени, в два раза больший длительности встречи Б и П2 , одновременно пришли оба пешехода. Найти скорость пешехода П1 .
Смотреть решение
12. Найдите наименьшее значение функции \( y=\frac{x^3+x^2+9}{x}-x^2 \)на отрезке [1;10]
Смотреть решение
