1. С двух полей, первое из которых по площади вдвое меньше второго, собрали урожай свёклы. Средняя урожайность составила 150 ц/га, в то время, как на первом поле собрали по 156 ц/га. Какова урожайность свёклы на втором поле?
Смотреть решение
2. На рисунке показан график зависимости высоты пирога от времени его нахождения в духовке. По горизонтальной оси откладывается время в часах, по вертикальной – высота в см. Пока пирог не поднимется хотя бы в 1,5 раза, духовку открывать нельзя. Определите по графику, через какое минимальное время можно будет открыть духовку. Ответ дайте в часах.

Смотреть решение
3. Основания равнобедренной трапеции равны 9 и 21, боковая сторона 10. Найдите длину диагонали трапеции.
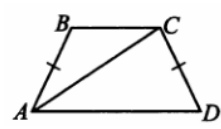
Смотреть решение
4. Из полной колоды карт (52 листа) вынимают сразу две карты. Одну из них смотрят – она оказалась дамой. После этого две вынутые карты перемешивают и одну из них берут наугад. Найти вероятность того, что она окажется тузом. Результат округлите до сотых.
Смотреть решение
5. Решите уравнение \( log_{sin\frac{\pi}{4}}(x+2)=4 \)
Смотреть решение
6. На боковой стороне CB равнобедренного (AB=BC) треугольника ABC выбрана точка K. Оказалось, что CA= AK =KB. Найдите ∠ ABC. Ответ дайте в градусах.

Смотреть решение
7. На рисунке изображен график y=f(x) функции . На оси абсцисс отмечены точки ‐2;2;3;4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

Смотреть решение
8. Цилиндрическая кастрюля, диаметр дна которой равен 30 см, наполнена водой. Какое минимальное число кастрюль той же высоты и с диаметром дна, равным 15 см, потребуется для того, чтобы перелить в них эту воду?
Смотреть решение
9. Найдите значение выражения \( (3^{\sqrt{7}}*(\frac{1}{3})^{\sqrt{5}})^{\sqrt{7}+\sqrt{5}} \)
Смотреть решение
10. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат
выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: \( F_{A}=pgl^3 \) , где l – длина ребра куба в метрах, p=1000 кг/м3 – плотность воды, а g – ускорение свободного падения (считайте g =10 Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 33750 Н? Ответ выразите в метрах.
Смотреть решение
11. Три автоматические линии выпускают одинаковую продукцию, но имеют разную производительность. Производительность всех трёх одновременно действующих линий в 1,5 раза выше производительности первой и второй линий, работающих одновременно. Сменное задание для первой линии вторая и третья линии, работая одновременно, могут выполнить на 4 ч 48 мин быстрее, чем его выполняет первая линия; это же задание вторая линия выполняет на 2 ч быстрее по сравнению с первой линией. Найти время выполнения первой линией своего сменного задания.
Смотреть решение
12. Найдите наименьшее значение функции \( f(x)=(x-2)(x-1)(x+1)(x+2) \) на [-1;2]
Смотреть решение
