1. Площади участков земли относятся как 4 : 3 : 5. Средняя урожайность всех трёх участков одинакова и составляет 28 ц зерна с гектара. Известно, что с третьего участка собрано на 84 ц зерна больше, чем с первого. Определите площадь первого участка.
Смотреть решение
2. На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали – значение температуры в градусах Цельсия. Сколько часов во второй половине дня температура не превышала
300С?

Смотреть решение
3. На стороне ВС прямоугольника ABCD, у которого АВ=20, AD=41, отмечена точка К так, что ∡AKB=45,Найдите KD.
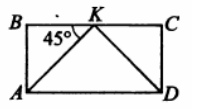
Смотреть решение
4. В урне два белых и три черных шара. Два игрока поочередно вынимают из урны по шару, не возвращая их обратно. Выигрывает тот, кто раньше получит белый шар. Найдите вероятность того, что выиграет игрок, который начинал вынимать шары.
Смотреть решение
5. Решите уравнение \( (x^2-36)^2+(x^2+4x-12)^2=0 \)
Смотреть решение
6. Угол между биссектрисой и высотой прямоугольного треугольника, опущенными на гипотенузу, равен 9. Во сколько раз больший острый угол этого треугольника
превосходит меньший?
Смотреть решение
7. На рисунке изображен график неравномерного прямолинейного движения тела (материальной точки). По оси абсцисс откладывается время в секундах, по оси ординат – расстояние в метрах. Найдите среднюю скорость этого тела на участке АВ (т.е. с 11‐й по 15‐ю секунду его движения включительно). Ответ дайте в км/час.
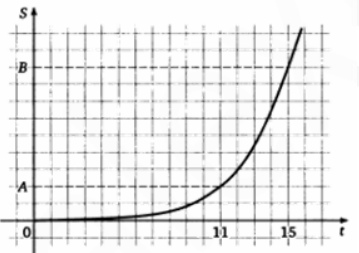
Смотреть решение
8. Найдите объём треугольной пирамиды DABC, если AB=30, BC =CA=17 и двугранные
углы при основании равны 45.
Смотреть решение
9. Найдите 8sina, если tga=0,75 и -pi<a<-pi/2
Смотреть решение
10. Высота над землей подброшенного вверх мяча меняется по закону h(t)=2,04+7t-4t^2, где h – высота в метрах, t – время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее четырёх метров?
Смотреть решение
11. Из пункта A по одному и тому же маршруту одновременно выехали грузовик и легковой автомобиль. Скорость легкового автомобиля постоянна и составляет 6/5
скорости грузовика. Через 30 минут вслед за ними из того же пункта выехал мотоциклист со скоростью 90 км/час. Найти скорость легкового автомобиля, если известно, что мотоциклист догнал грузовик на один час раньше, чем легковой автомобиль.
Смотреть решение
12. Найдите наименьшее значение функции \( y=x+\frac{25}{x}+2020 \) на отрезке [1;25]
Смотреть решение
