1. На склад привезли 126 тонн яблок, груш и слив. Яблок оказалось в 4 раза больше, чем груш. Слив на 18 тонн меньше, чем груш. Сколько тонн яблок привезли на склад?
Смотреть решение
2. На графике показано изменение давления в паровой турбине после запуска. На оси абсцисс откладывается время в минутах, на оси ординат – давление в атмосферах. Определите по графику, сколько минут давление было больше 5 атмосфер.
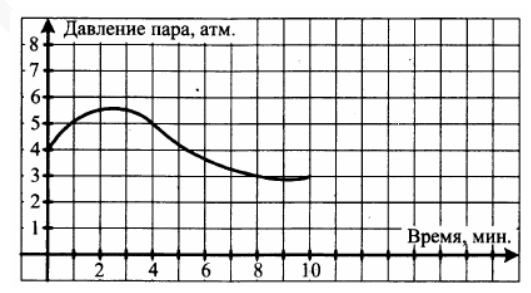
Смотреть решение
3. На окружности с центром О отмечены точки А и В так, что ∠AOB 78 . Длина меньшей дуги АВ равна 39 мм. Найдите длину большей дуги в мм.
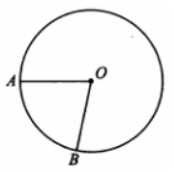
Смотреть решение
4. В урне 5 белых и 6 черных шаров. Из урны вынули один шар и, не глядя, отложили в сторону. После этого из урны взяли еще один шар. Он оказался белым. Найдите вероятность того, что первый шар, отложенный в сторону, ‐ тоже белый.
Смотреть решение
5. Решите уравнение ||4-x^2|-x^2|=1. В ответе укажите сумму корней этого уравнения.
Смотреть решение
6. На окружности отмечены точки А и В так, что меньшая дуга АВ равна 720. Прямая ВС касается окружности в точке В так, что угол АВС острый. Найдите угол АВС. Ответ дайте в градусах.
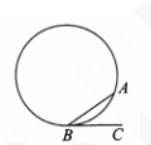
Смотреть решение
7. На рисунке изображён график производной функции y=f'(x) определённой на интервале (–4; 5). Найдите сумму абсцисс точек экстремума функции f(x).
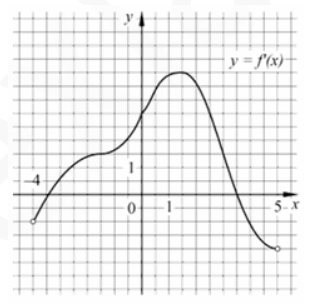
Смотреть решение
8. Найдите расстояние между вершинами B1 и D2 изображённого на рисунке многогранника. Все двугранные углы многогранника прямые.
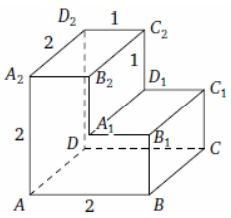
Смотреть решение
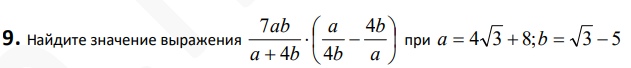
Смотреть решение
10. Дверь люка устроена так, что может поворачиваться в шарнире без трения, удерживается в горизонтальном положении тросом. Сила натяжения троса рассчитывается по формуле: \( F=\frac{mg}{2}*\frac{1}{sina} \)где m — масса двери, выраженная в килограммах, g = 9,8 Н/кг, ускорение свободного падения , a = 30° — угол, образованный тросом и дверью. Какую максимальную массу может иметь дверь, чтобы сила натяжения троса не превосходила 245Н?
Смотреть решение
11. Грузовик и гоночный автомобиль выехали одновременно из пункта A и должны прибыть в пункт C. Грузовик, двигаясь с постоянной скоростью, доехал до пункта C, проделав путь, равный 360 км. Гоночный автомобиль поехал по окружной дороге и сначала доехал до пункта B, расположенного в 120 км от пункта A, двигаясь со скоростью, вдвое большей скорости грузовика. После пункта B он увеличил свою скорость на 40 км/ч и проехал путь от пункта B до пункта C, равный 1000 км. Он прибыл в пункт C на 1 час 15 минут позднее грузовика. Если бы гоночный автомобиль весь свой путь от пункта A до пункта C ехал с той же скоростью, что и от пункта B до пункта C, то в пункт C он прибыл бы на 1 час позднее грузовика. Найти скорость грузовика.
Смотреть решение
12. Найдите наименьшее значение функции y=2(x-20)√(x+7)+5 на отрезке [‐6;2].
Смотреть решение
