1. Холодильник имеет форму прямой призмы, в основании которой квадрат со
стороной 60 см. 40% объема холодильника занимает холодильная камера, состоящая
из трех ящиков в форме прямоугольного параллелепипеда, каждый размером 0,6м х
0,6м х 0,3м. Найдите высоту холодильника. Ответ выразите в метрах.
Смотреть решение
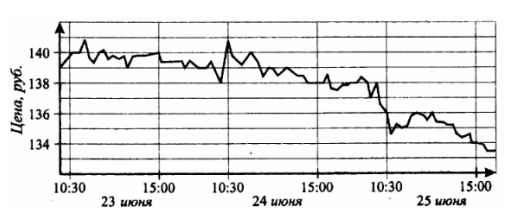
2. На графике показано изменение биржевой стоимости в рублях акций компании
“Распадская” в период с 23 июня по 25 июня. Рабочий день на бирже начинается в
10:30. Бизнесмен купил 230 акций компании “Распадская” 23 июня до 15:00, а продал
их 25 июня между 10:30 и 15:00. Какой наименьший убыток он мог понести? Ответ
дайте в рублях.
Смотреть решение
3. Найдите площадь треугольника ACD (см. рисунок)
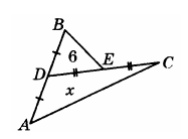
Смотреть решение
4. Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах
равна 0,875. Какова вероятность попадания при одном выстреле?
Смотреть решение
5. Найдите сумму всех корней уравнения \( (2(x-2)(x+2))^{1/3}=x-2 \)
Смотреть решение
6. Известно, что точки К и М лежат соответственно на сторонах АВ и ВС треугольника АВС, а О – точка пересечения АМ и СК. Известно, что площади треугольников АОК и СОМ равны соответственно 1 и 8, а треугольник АОС и четырехугольник ВКОМ равновелики. Найдите площадь треугольника АВС.

Смотреть решение
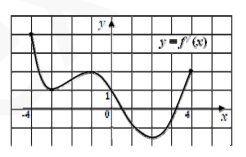
7. Функция у = f (x) определена на промежутке [‐4; 4]. На рисунке приведен график её
производной. Найдите количество точек графика функции у = f (x), касательная в которых
образует с положительным направлением оси Ох угол 50.
Смотреть решение
8. Объем правильной шестиугольной призмы равен 180. Сначала каждое ее боковое ребро увеличили в два раза, а затем каждую сторону каждого основания уменьшили в три раза. Найдите объем полученной призмы.
Смотреть решение
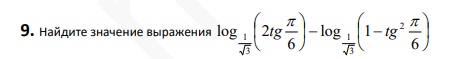
Смотреть решение
10. Камнеметательная машина выстреливает камни под некоторым острым углом к
горизонту. Траектория полета камня описывается формулой y=ax^2+bx где a=-1/625 м^2, b=6/25 постоянные параметры, x (м) – смещение камня по горизонтали, y (м) – высота камня над землей. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 5,7 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1,34 метра?
Смотреть решение
11. В магазине продано 12 тонн орехов трёх сортов по цене соответственно 2 руб., 4
руб. и 6 руб. за 1 кг на общую сумму 42 тыс. руб. Известно, что количества тонн
проданных орехов соответственно первого, второго и третьего сортов образуют
арифметическую прогрессию. Сколько тонн орехов второго сорта продано в магазине?
Смотреть решение
12. При каком наибольшем значении функция f(x)=x^3+bx^2+3bx-1 возрастает на всей числовой прямой?
Смотреть решение
