1. Под строительную площадку отвели участок прямоугольной формы. При
утверждении плана застройки ширину участка уменьшили на 20%, а длину увеличили
на 20%. На сколько процентов уменьшилась площадь участка после утверждения
плана застройки?
Смотреть решение
2. Пенсионер Геннадий Васильевич не первый год живёт в России и помнит цены
2000г. После очередной индексации пенсии он строит график цен в рублях
(отмеченных на оси ординат) на 7 продуктов (отмеченных на оси абсцисс), где первым
столбцом идёт цена на продукт в 2000 году, а вторым — цена в 2019 году. Глядя на
график, он решает круто изменить свою жизнь, отказавшись от продуктов, стоимость
которых в 2019 году стала больше, чем стоимость бутылки молока. Однако для водки
Геннадий Васильевич решил сделать исключение ввиду того, что считает ее жизненно‐
важным продуктом.
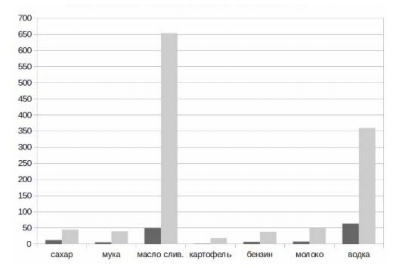
От скольких продуктов из указанных на графике откажется в итоге Геннадий
Васильевич?
Смотреть решение
3. Найдите площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1х1 см. Ответ дайте в см2.

Смотреть решение
4. На первый курс экономического факультета Российского заборостроительного
университета было зачислено 45 человек, в том числе Сюзанна Зайцева и Виолетта
Волкова. Студентов первого курса распределили по группам численностью 20 и 25
человек случайным образом. Найдите вероятность того, что Сюзанна и Виолетта
окажутся в одной группе. Ответ округлите до тысячных.
Смотреть решение
5. Решите уравнение \( \sqrt{2+lgx}=lgx \)Если уравнение имеет более одного корня, в
ответе укажите меньший из них.
Смотреть решение
6. Концы отрезка АВ лежат по разные стороны от прямой . Расстояние от точки А до
прямой l равно 23, а расстояние от точки В до прямой l равно 45. Найдите
расстояние от середины отрезка АВ до прямой l .
Смотреть решение
7. На рисунке изображен график функции y=f'(x), где f'(x) – производная функции y=f(x)
В какой из точек ‐3; ‐2; ‐1; 0; 1 значение функции наибольшее? В ответе укажите эту точку.

Смотреть решение
8. В кубе ABCDA1B1C1D1 со стороной 6 вычислите квадрат расстояния между точками К и М – серединами сторон AD и СС1 соответственно.
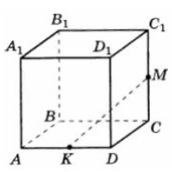
Смотреть решение
9. Найдите значение выражения \( \frac{b^2*b^{1/6}}{b^{1/10}*b^{1/15}} \)при b=6
Смотреть решение
10. Приближаясь к посту ГИБДД со скоростью 60 км/ч, таксист Рушан увидел в 30
метрах впереди инспектора ДПС Кулебякина, который жезлом указывал ему
остановиться. Немедленно нажав на тормоз, Рушан полностью остановился через 3
секунды. Сколько метров не доехал Рушан до инспектора Кулебякина? Скорость,
пройденный путь и ускорение торможения связаны соотношениями
\( v=at \); \( s=vt-\frac{at^2}{2} \), где (м/с) ‐ начальная скорость, (м/с2) ‐ ускорение, (м)
‐ путь, пройденный до полной остановки, (с) ‐ время от начала торможения до полной остановки
Смотреть решение
11. Для того, чтобы успеть к началу занятий в университете по московским пробкам,
Сюзанна Зайцева выезжает из дома на своем автомобиле «Бугатти» в 8:30. Расстояние
до университета 20 км. Весь путь Сюзанна едет с постоянной скоростью. Однако,
проехав 15 км, Сюзанна вспомнила, что надела туфли не одного цвета с сумочкой.
Мгновенно развернувшись, Сюзанна поехала обратно домой, но из‐за пробки ей
пришлось снизить скорость на 50 км/ч. Приехав домой и проведя там 15 минут,
Сюзанна поехала в университет с той же скоростью, что и в первый раз. Найдите эту
скорость (в км/ч), если Сюзанна приехала в университет ровно к началу занятий в
10.00.
Смотреть решение
12. Найдите наименьшее значение функции \( y=3cosx-\frac{48}{\pi}x+19 \) на отрезке [-2/3pi;0]
Смотреть решение
