1. Шоколадка стоит 31 рубль. В воскресенье в супермаркете действует специальное
предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок).
Сколько шоколадок можно получить на 230 рублей в воскресенье?
Смотреть решение
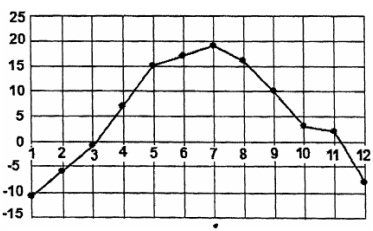
2. На диаграмме изображено среднемесячное значение температуры в Москве за
1976 год. По оси абсцисс отложены месяцы, а по оси ординат – среднемесячное
значение температуры в 0С. Для наглядности точки соединены линией. Пользуясь
диаграммой, выясните, сколько месяцев значение этой температуры было от ‐5С до
+5С?
Смотреть решение
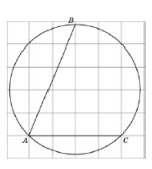
3. Найдите градусную меру дуги BC окружности, на которую
опирается угол BAC. Ответ дайте в градусах.
Смотреть решение
4. Страховая компания в некотором регионе страхует владельцев автомобилей. Цена
годового страхового полиса равна 35 000 рублей. Исследования показали, что в
течение года владелец автомобиля попадает в мелкую аварию с вероятностью 0,16 и
средняя сумма страховой выплаты при этом равна 40 000 рублей. С вероятностью
0,035 автомобилист попадает в более серьезную аварию, и средняя сумма выплаты
при этом равна 700 000 рублей. Найдите математическое ожидание случайной
величины «средний доход страховой компании от продажи одного полиса»
Смотреть решение
5. Решите уравнение \( \frac{14-x}{x-2}=\frac{x^2+4x}{x-2} \) . Если уравнение имеет более одного корня, то в ответ запишите наибольший.
Смотреть решение
6. В треугольнике АВС сторона BC равна 6, медиана AM равна 3. Найдите угол BAC.
Ответ дайте в градусах.
Смотреть решение
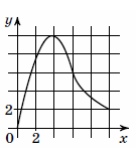
7. Материальная точка движется вдоль прямой от начального до конечного положения. На рисунке изображен график ее движения. На оси абсцисс откладывается время в
секундах, на оси ординат – расстояние от начального положения точки (в метрах). Найдите среднюю скорость движения точки. Ответ дайте в метрах в секунду.
Смотреть решение
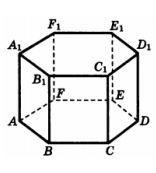
8. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 площадь основания равна 13, а боковое ребро равно 12. Найдите объем призмы ACDFA1C1D1F1.
Смотреть решение
9. Найдите значение выражения \( sin800*sin900*sin1000 \)
Смотреть решение
10. Расстояние h, пройденное свободно падающим телом, вычисляется по формуле:
\( h=\frac{gt^2}{2} \) , где g = 10 м/с2 (ускорение свободного падения), t – время в секундах.
Какое расстояние свободно падающее тело пройдёт за третью секунду своего
падения? Ответ дайте в метрах
Смотреть решение
11. Расстояние между городами А и В равно 80 км. Из А в В выехала машина, а через
20 минут – мотоциклист, скорость которого равна 90 км/ч. Мотоциклист догнал
машину в пункте С и повернул обратно. Когда машина прибыла в В, мотоциклист
проехал половину пути от С до А. Найти расстояние от С до А.
Смотреть решение
12. Найдите наибольшее значение функции \( y(x)=sin(2x+\frac{\pi}{6}) \) на промежутке \( [-\frac{\pi}{2};\frac{\pi}{2}] \)
Смотреть решение
