1. В январе весы стоили 2800 рублей. В феврале они подешевели на 15%, а в марте —
ещё на 5%. Сколько рублей стали стоить весы в апреле?
Смотреть решение
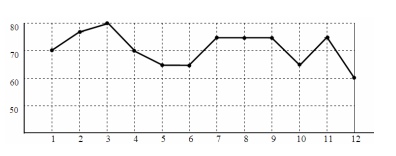
2. На графике точками отмечена цена (в рублях) одного литра подсолнечного масла
«Злато» в одном из супермаркетов Липецка течение первых 12 дней июля. Для
наглядности точки соединены отрезками. Определите размах цен (в рублях) на
подсолнечное масло «Злато» за указанный период.
Смотреть решение
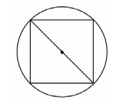
3. В окружность с диаметром 3√2 вписан квадрат.
Найдите сторону квадрата.
Смотреть решение
4. Вероятность, что два случайно взятых лотерейных билета окажутся выигрышными,
составляет 0,04. Какова вероятность, что хотя бы один из двух билетов окажется
выигрышным?
Смотреть решение
5. Найдите корень уравнения \( 4^{\frac{x}{3}}=\frac{\sqrt{2}}{2} \)
Смотреть решение
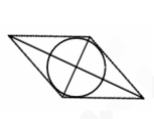
6. Диагонали ромба равны 2√5 и 4√5. Найдите
радиус вписанной в ромб окружности.
Смотреть решение
7. Материальная точка движется прямолинейно по закону \( x(t)=\frac{1}{3}t^3-3t^2-5t+3 \) , где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Смотреть решение
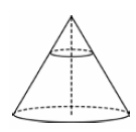
8. Площадь основания конуса равна 45. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 4 и 8, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Смотреть решение
9. Известно, что \( \frac{cosx-sinx}{cosx+sinx}=-0,8 \). Найти \( tgx \)
Смотреть решение
10. Датчик сконструирован таким образом, что его антенна ловит радиосигнал,
который затем преобразуется в электрический сигнал, изменяющийся со временем по
закону \( U=U_{0}sin(wt+φ) \) , где t- время в секундах, амплитуда \( U_{0}=2 \) В , частота \( w=150 \),\( φ=45 \)фаза . Датчик настроен так, что если напряжение в нём не
ниже чем 1 В, то загорается лампочка. Какую часть времени (в процентах) на
протяжении первой секунды после начала работы лампочка будет гореть?
Смотреть решение
11. Имеется два сосуда равного объёма. Первый наполнен раствором соли с
концентрацией 44%, второй – раствором соли с концентрацией 66%. Из каждого
сосуда взяли по 5,5 л раствора; взятое из первого сосуда вылили во второй, а взятое из
второго – в первый, после чего концентрации растворов в сосудах стали равны.
Сколько литров раствора было в первом сосуде?
Смотреть решение
12. Найти наибольшее значение функции \( f(x)=cos\pi x-6x \) на отрезке [-2/3;1]
Смотреть решение
