1. В июне 1 кг огурцов стоил 50 рублей. В июле огурцы подешевели на 20%, а в
августе еще на 50%. Сколько рублей стоил 1 кг огурцов после снижения цены в
августе?
Смотреть решение
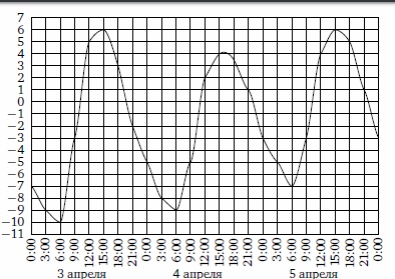
2. На рисунке показано, как изменялась температура воздуха с 3 по 5 апреля. По
горизонтали указано время суток, по вертикали — значение температуры в градусах
Цельсия. Найдите разность между наименьшим и наибольшим значениями температуры в
первой половине суток 5 апреля. Ответ дайте в градусах Цельсия.
Смотреть решение
3. Найдите тангенс угла В треугольника АВС, изображенного на рисунке
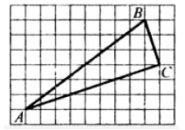
Смотреть решение
4. Три друга А., Б. и В. летят на самолете. При регистрации им достались три кресла
подряд, и друзья заняли их в случайном порядке. Найдите вероятность того, что А.
сидит рядом с Б. Ответ округлите до сотых.
Смотреть решение
5. Решите уравнение \( cos\frac{\pi x}{6}=-0,5 \) В ответе запишите наибольший отрицательный
корень уравнения.
Смотреть решение
6. Найдите величину тупого угла между биссектрисами острых углов прямоугольного
треугольника. Ответ дайте в градусах.
Смотреть решение
Смотреть видео решение
7. Прямая, изображенная на рисунке, является графиком одной из первообразных функции \( y=f(x) \). Найдите \( f(2) \).
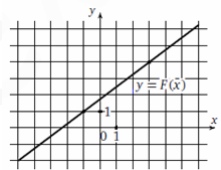
Смотреть решение
8. Дан куб ABCDA1B1C1D1. Площадь четырёхугольника ABC1D1 равна 4√2 . Найдите
площадь поверхности куба.
Смотреть решение
9. Найдите значение выражения \( x+3+\sqrt{x^2-6x+9} \) при \( x=0,31 \)
Смотреть решение
10. Небольшой мячик бросают под острым углом к плоской горизонтальной
поверхности земли. Расстояние (в метрах), которое пролетает мячик, вычисляется по
формуле \( L=\frac{V_{0}}{g}sin2a \) где v0 = 20 м/с – начальная скорость мячика, а ‐
ускорение свободного падения (считайте g = 10 м/с2). При каком наименьшем
значении угла (в градусах) мячик перелетит реку шириной 20 м?
Смотреть решение
11. Собственная скорость теплохода равна 20 км/ч, скорость течения реки равна 4
км/ч. Теплоход проплыл от одной пристани до другой и вернулся обратно. Найдите
среднюю скорость теплохода на протяжении всего пути. Ответ дайте в км/ч.
Смотреть решение
12. В какой точке отрезка [12; 22] первообразная для функции \( f(x)=-1-ln^2(x-2) \) достигает своего наименьшего значения на этом отрезке.
Смотреть решение
