1. Выпускники 11 «Б» класса покупают букеты цветов для последнего звонка: из 5 роз
каждому учителю и из 7 роз классному руководителю и директору. Они собираются
подарить цветы 18 учителям (включая директора и классного руководителя), розы
покупаются по оптовой цене 25 рублей за штуку. Сколько рублей стоят все розы?
Смотреть решение
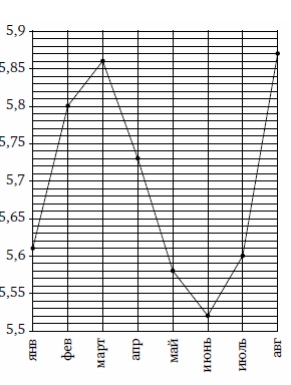
2. На рисунке жирными точками показан среднемесячный курс китайского юаня с января по август 2014 года. По горизонтали указываются месяцы, по вертикали — цена юаня в рублях. Для
наглядности жирные точки соединены ломаной линией. Определите по рисунку разность
курса юаня в августе и июле. Ответ дайте в рублях.
Смотреть решение
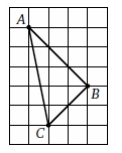
3. На клетчатой бумаге изображён треугольник ABC. Найдите
величину его наибольшего угла. Ответ выразите в градусах.
Смотреть решение
4. Чтобы поступить в институт на специальность «Международное право», абитуриент
должен набрать на ЕГЭ не менее 60 баллов по каждому из трех предметов—
математика, русский язык и иностранный язык. Чтобы поступить на специальность
«Социология», нужно набрать не менее 60 баллов по каждому из трех предметов—
математика, русский язык и обществознание. Вероятность того, что абитуриент А.
получит не менее 60 баллов по математике, равна 0,8, по русскому языку—0,9, по
иностранному языку—0,8 и по обществознанию—0,9. Найдите вероятность того, что А.
поступит хотя бы на одну из двух упомянутых специальностей.
Смотреть решение
5. Решите уравнение \( x=\frac{20x+25}{x+20} \) Если уравнение имеет более одного корня, в
ответе запишите меньший из корней.
Смотреть решение
6. В треугольнике ABC известно, что AC=5√5,tgA=2,tgC=3. Найдите AB.
Смотреть решение
7. Прямая y=-3x+8 параллельна касательной к графику функции y=x^2+7x-6. Найдите абсциссу точки касания.
Смотреть решение
8. Площадь полной поверхности призмы на 24 см2 больше площади её боковой
поверхности. Найдите площадь основания призмы. Ответ дайте в квадратных
сантиметрах.
Смотреть решение
9. Найдите значение выражения \( \frac{b^3*b^{\frac{2}{5}}}{b^{\frac{6}{5}}*b^{3,2}} \) при \( b=\frac{5}{7} \)
Смотреть решение
10. Груз массой 0,4 кг колеблется на пружине. Его скорость v меняется по закону \( v=v_{0}sin\frac{2 \pi t}{T} \), где ‐время с момента начала колебаний, ‐ период
колебаний T=12 с, v0 =1 м/с . Кинетическая энергия Е (в джоулях) груза вычисляется по
формуле \( \frac{mv^2}{2} \), где ‐ m масса груза (в килограммах), ‐ v скорость груза (в
метрах в секунду). Найдите кинетическую энергию груза через 5 с после начала
колебаний. Ответ дайте в джоулях.
Смотреть решение
11. Два тела движутся по окружности в одну сторону. Первое проходит круг на 2
минуты быстрее второго и догоняет второе каждый час. За сколько минут второе тело
проходит один круг?
Смотреть решение
12. Найдите наименьшее значение функции \( y=2^{\sqrt{x}}+3^{x^{\frac{1}{3}}}+4 \) на отрезке [1;64]
Смотреть решение
