1. Маша отправила СМС‐сообщения с новогодними поздравлениями своим 16
друзьям. Стоимость одного СМС‐ сообщения—1 рубль 30 копеек. Перед отправкой
сообщений на счете у Маши было 30 рублей. Сколько рублей останется у Маши на
счете после отправки всех сообщений?
Смотреть решение
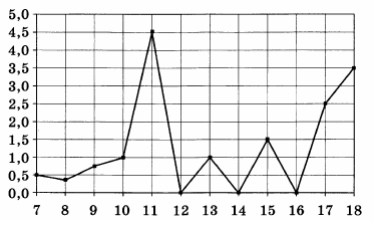
2. На рисунке жирными точками показано суточное количество осадков, выпадавших
в Элисте с 7 по 18 декабря 2001 года. По горизонтали указываются числа месяца, по
вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах.
Для наглядности жирные точки на рисунке соединены линией. Определите по
рисунку, сколько дней за данный период не выпадало осадков.
Смотреть решение
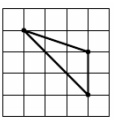
3. На клетчатой бумаге с размером клетки √5*√5 изображён треугольник. Найдите радиус его описанной окружности.
Смотреть решение
4. Монету бросают восемь раз. Во сколько раз событие «орел выпадает ровно 6 раз»
более вероятно, чем событие «орел выпадет ровно один раз» ?
Смотреть решение
5. Найдите корень уравнения \( 3^x*4^x=144^{x-2} \)
Смотреть решение
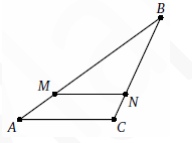
6. На сторонах AB и BC треугольника ABC выбраны точки M и N соответственно так, что MN || AC. Найдите AC, если NM =9, NC =4 и NB= AC.
Смотреть решение
7. Материальная точка движется прямолинейно по закону \( x(t)=\frac{t^3}{3}-\frac{3t^2}{2}-3t+17 \)(где x —расстояние от точки отсчета в метрах, —время в секундах, измеренное с
начала движения). В какой момент времени ее скорость была равна 15 м/с?
Смотреть решение
8. Основанием наклонной призмы ABCDA1B1C1D1 является квадрат ABCD, а диагональ
A1C призмы перпендикулярна плоскости основания. Найдите площадь основания
призмы, если \( A_{1}A=3\sqrt{33} \), \( CA_{1}=15 \)
Смотреть решение
9. Найдите значение выражения \( 4^{-13}:56^{-15}*14^{-14} \)
Смотреть решение
10. Автомобиль, двигавшийся со скоростью v0 = 27 м/с, начал торможение с
постоянным ускорением a = 5,4 м/с2. Определите время, прошедшее от момента
начала торможения до полной остановки, если известно, что за это время автомобиль
проехал 81 м. Тормозной путь, время торможения и ускорение связаны формулой \( S=v_{0}t-\frac{at^2}{2} \)Ответ выразите в секундах.
Смотреть решение
11. Из городов A и B навстречу друг другу одновременно выехали с постоянными
скоростями два автомобиля. Скорость первого автомобиля была в полтора раза
больше скорости второго. Второй автомобиль прибыл в A на 5 часов позже, чем
первый прибыл в B. На сколько минут раньше произошла бы встреча автомобилей,
если бы второй автомобиль ехал с той же скоростью, что и первый?
Смотреть решение
12. Найдите наименьшее значение функции \( y=log_{\sqrt{3}}(x-4\sqrt{x-2}+5) \) на
отрезке [5;10].
Смотреть решение
