1. Необходимо перевезти 50 скутеров весом 300 килограмм каждый. Сколько рейсов
понадобится сделать для этого, используя машину грузоподъемностью 5 тонн?
Смотреть решение
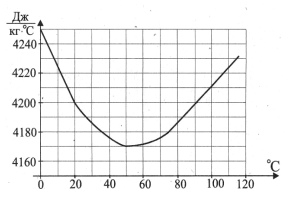
2. На графике показано изменение удельной теплоёмкости водного раствора
некоторого вещества в зависимости от температуры. По горизонтали указывается
температура в градусах Цельсия, по вертикали – удельная теплоёмкость в Дж/кг*C .
Определите по рисунку, на сколько изменится удельная теплоемкость при нагревании
раствора с 20° до 100°. Ответ дайте в Дж/кг*C
Смотреть решение
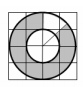
3. Площадь маленького круга равна 4. Найдите площадь
закрашенной фигуры.
Смотреть решение
4. В классе учится 16 человек: 6 мальчиков и 10 девочек. Перед началом уроков
классный руководитель случайным образом выбирает двух учащихся класса для
дежурства в столовой. Какова вероятность, что дежурить в столовую отправятся
мальчик с девочкой?
Смотреть решение
5. Найдите корень уравнения \( \sqrt{3-x}=1-x \) Если корней несколько, то в ответе
укажите больший из них.
Смотреть решение
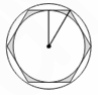
6. Радиус окружности, описанной около правильного шестиугольника,
равен √3 . Найдите радиус вписанной окружности.
Смотреть решение
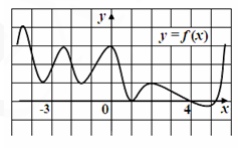
7. По графику функции у = f(x) определите количество точек на интервале (‐3; 4), в которых
касательная к графику параллельна прямой у=0,3х – 4 или совпадает с ней.
Смотреть решение
8. Объем правильной шестиугольной призмы равен 180. Сначала каждое ее боковое ребро увеличили в два раза, а затем каждую сторону каждого основания уменьшили в три раза. Найдите объем полученной призмы.
Смотреть решение
9. Найдите значение выражения \( log_{\frac{4}{25}}(log_{4}(32)) \)
Смотреть решение
10. Максимальная высота подъёма тела, брошенного под углом к горизонту,
вычисляется по формуле \( h=\frac{(v*sina)^2}{2g} \), где v (м/c) – начальная скорость тела, α
– угол, под которым тело брошено к горизонту, g – ускорение свободного падения
(считать, что g=10 м/с2). С какой скоростью необходимо бросить мяч под углом 30º к
горизонту, чтобы он поднялся на высоту 5 м?
Смотреть решение
11. Сцепленные зубчатые колеса вместе в сумме делают 240 оборотов в минуту.
Найдите количество зубьев у второго колеса, если у первого их 100, и делает оно на 80
оборотов в минуту больше, чем второе колесо.
Смотреть решение
12. Найдите наибольшее значение функции \( y=(x-1)2^x \) на отрезке [2; 6].
Смотреть решение
