1. В салоне парфюмерии проходит акция: покупая флакон духов объёмом 100 мл,
покупатель получает в подарок флакон духов объёмом 30 мл. Какой наибольший
объём (в мл) духов можно получить за 7000 рублей во время этой акции, если флакон
духов объёмом 100 мл стоит 1800 рублей, объёмом 50 мл – 1200 рублей, а объёмом
30 мл – 800 рублей?
Смотреть решение
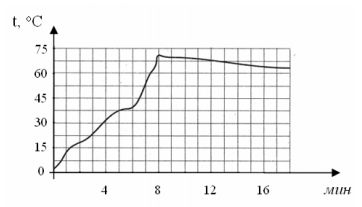
2. На графике показан процесс разогрева двигателя легкового автомобиля при
температуре окружающего воздуха 5°С. На оси абсцисс откладывается время в
минутах, прошедшее от запуска двигателя, на оси ординат – температура двигателя в
градусах Цельсия. Когда температура достигает определённого значения, включается
вентилятор, охлаждающий двигатель, и температура начинает понижаться. Опреде‐
лите по графику, сколько минут прошло с момента запуска двигателя до включения
вентилятора?
Смотреть решение
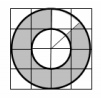
3. Площадь большого круга равна 24. Найдите площадь
закрашенной фигуры.
Смотреть решение
4. В случайном эксперименте бросают три игральные кости. Найдите вероятность
того, что в сумме выпадет 16 очков. Результат округлите до сотых.
Смотреть решение
5. Найдите корень уравнения \( (\frac{1}{8})^{-3+x}=512 \)
Смотреть решение
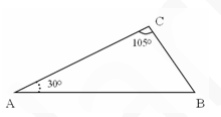
6. В треугольнике АВС угол А равен 30, а угол С равен 105. Найдите АС, если ВС= 3√2 .
Смотреть решение
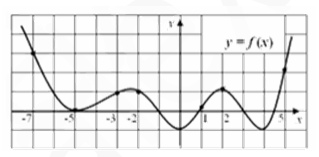
7. На графике функции у = f (x) отмечены семь точек с абсциссами ‐7, ‐5, ‐3, ‐2, 1, 2,
5. Определите по данному графику, в какой из этих точек значение производной f′(x)
наибольшее. (В ответе укажите абсциссу этой точки).
Смотреть решение
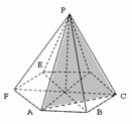
8. В правильной шестиугольной пирамиде PАВСDEF сторона основания равна 2, а боковое ребро равно √6. Найдите площадь сечения пирамиды плоскостью РАС.
Смотреть решение
9. Найдите значение выражения \( 6x*(3x^{12})^3:(3x^9)^4 \) при \( x=75 \)
Смотреть решение
10. При вращении ведёрка с водой на верёвке в вертикальной плоскости вода не
выливается из него, если сила её давления на дно ведёрка неотрицательна во всех
точках траектории. В верхней точке траектории сила давления воды на дно
минимальна и равна \( P=m(\frac{V^2}{L}-g)H \), где m – масса воды в кг, v – скорость движения
ведёрка в м/с, L – длина веревки в метрах, g = 10 м/с2 – ускорение свободного
падения. С какой минимальной скоростью v надо вращать ведёрко, чтобы вода не
выливалась из него, если длина веревки равна 57,6 см? Ответ дайте в м/с.
Смотреть решение
11. Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов
теста, а Ваня — на 9. Они одновременно начали отвечать на вопросы теста, и Петя
закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест?
Смотреть решение
12. Найдите наименьшее значение функции \( f(x)=x^3-3x^2-9x+31 \) на отрезке [-1;4]
Смотреть решение
