13. а) Решите уравнение \( sinx=cos^2x+0,5log_{\sqrt{2}}(2) \)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-0,5π;π]
Смотреть решение
14. В основании SABCD лежит прямоугольник ABCD со сторонами AB=4 и
BC=√33, все боковые ребра пирамиды равны 4. На диагонали BD основания ABCD
отмечена точка Е, а на ребре AS – точка F так, что SF=BE=3 .
А) Докажите, что плоскость CEF параллельна SB.
Б) Пусть плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от Q до
плоскости АВС.
Смотреть решение
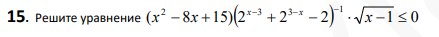
Смотреть решение
16. Дан выпуклый четырехугольник ABCD с прямым углом А. Окружность,
проходящая через вершины А, В и D пересекает стороны ВС и CD в точках M и N
соответственно. Прямые BN и DM пересекаются в точке Р, а прямая СР пересекает
сторону AD в точке К.
А) Докажите, что точки А, М, Р и К лежат на одной окружности.
Б) Найдите радиус этой окружности, если известно, что прямая СK параллельна
прямой АМ и АВ=АК=KD=4√5
Смотреть решение
17. Банк планирует на один год вложить 30 % имеющихся у него средств клиентов в
проект А, а остальные 70 % – в проект B. В зависимости от обстоятельств проект А может
принести прибыль в размере от 32 % до 37 % годовых, а проект B – от 22% до 27%
годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им процент по
заранее установленной ставке, уровень которой должен находиться от 10% до 20%
годовых. Определите, какую наименьшую и наибольшую чистую прибыль в
процентах годовых от суммарных вложений в проекты А и B может при этом получить
банк.
Смотреть решение
