1. Подготовка книги к печати стоит 30 тыс. р. Печать одного экземпляра стоит 30 р.
Сеть книжных магазинов покупает эту книгу у издательства по 70 р. за экземпляр. При
каком наименьшем тираже книги издательство окажется не в убытке?
Смотреть решение
2. На рисунке изображён график среднесуточной температуры в г. Омске в период с
14 по 27 января 1974 г. На оси абсцисс откладываются числа месяца, на оси ординат —
температура в градусах Цельсия. Определите по графику, какой была наибольшая
среднесуточная температура в период с 14 по 21 января 1974 г. Ответ дайте в градусах
Цельсия.

Смотреть решение
3. На клетчатой бумаге с размером клетки 1 см x 1 см изображён четырёхугольник. Найдите его площадь. Ответ дайте в квадратных сантиметрах.
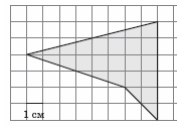
Смотреть решение
4. Поставщик заказывает опоры двигателя у двух фабрик. Первая фабрика выпускает
80% этих опор, вторая — 20 %. Первая фабрика выпускает 1 % бракованных опор, а
вторая — 5 %. Найдите вероятность того, что случайно заказанная у поставщика опора
двигателя будет исправной.
Смотреть решение
5. Решите уравнение \( 7^{3x-2}*7^{x-1}=7 \)
Смотреть решение
6. Радиус окружности равен 19. Найдите величину острого вписанного угла,
опирающегося на хорду, равную 19√2 . Ответ дайте в градусах.
Смотреть решение
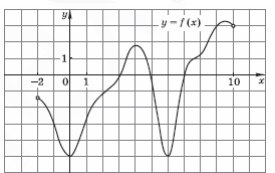
7. На рисунке изображён график функции y = f(x), определённой на
интервале (–2; 10). Определите количество точек с целыми абсциссами,
в которых производная функции отрицательна.
Смотреть решение
8. В правильной треугольной пирамиде сторона основания равна 42, высота равна
7√6 . Найдите плоский угол при вершине пирамиды. Ответ дайте в градусах.
Смотреть решение
9. Найдите значение выражения \( \frac{6\sqrt{x}+5}{\sqrt{x}}-\frac{5\sqrt{x}}{x}+3x-6 \) при \( x=6 \)
Смотреть решение
10. Для определения эффективной температуры звёзд используют закон Стефана—
Больцмана, согласно которому мощность излучения нагретого тела (Вт) вычисляется
по формуле \( P=σST^4 \), где σ=5,7*10^(-8) постоянная, S площадь поверхности тела (м2), T — температура тела (К). Известно, что некоторая звезда имеет
площадь поверхности \( S=\frac{1}{64}*10^{20} \) м^2, а излучаемая ею мощность \( P \) не менее \( 2,28*10^{25} \) Вт. Определите наименьшую возможную температуру этой звезды.
Ответ дайте в градусах Кельвина
Смотреть решение
11. Часы со стрелками показывают 11 ч 00 мин. Через сколько минут минутная
стрелка в двенадцатый раз поравняется с часовой?
Смотреть решение
12. Найдите точку максимума функции \( y=10x*cosx-7cosx-10sinx-4 \) принадлежащую промежутку (0;0,5π)
Смотреть решение
