13. а) Решите уравнение \( sin2x=sinx-2cosx+1 \)
б) Найдите все корни этого уравнения, принадлежащие промежутку [1,5π;3π]
Смотреть решение
14. В треугольной пирамиде ABCD длины всех рёбер равны. Точка Р равноудалена от
вершин А и D, причём известно, что PB=PC и прямая РВ перпендикулярна высоте
треугольника АСD, опущенной из вершины D.
а) Докажите, что точка Р лежит на пересечении высот пирамиды ABCD .
б) Вычислите объем пирамиды ABCD, если известно, что \( PB=\sqrt{\frac{3}{2}} \)
Смотреть решение
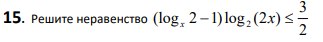
Смотреть решение *
16. В трапецию ABCD c основаниями ВС и AD вписана окружность с центром О, СН –
высота трапеции, Е – точка пересечения диагоналей.
А) Докажите, что ∠OHC=0,5∠ADC
Б) Найдите площадь четырехугольника CEOH, если известно, что ∠BAD=90, BC=9, AD=18.
Смотреть решение
17. В июле планируется взять кредит в банке на сумму 20 млн рублей на некоторый
срок (целое число лет). Условия его возврата таковы:
‐ каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;
‐ с февраля по июнь каждого года необходимо выплатить часть долга;
‐ в июле каждого года долг должен быть на одну и ту же величину меньше долга на
июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его
погашения равнялась 47 млн рублей?
Смотреть решение
